قبل محاولة الإجابة على هذا التساؤل ينبغي أن نلقي نظرة على شيء إسمه فيزياء الكم حتى نفهم مجريات المادة الزمنية إذا صح لها هذا التعبير
هي نظرية رئيسة في الفيزياء توفر وصفًا للخصائص الفيزيائية للطبيعة على مقياس الذرات والجسيمات دون الذرية.[2] وميكانيكا الكم (أو الحركة الكمومية) هي الأساس الذي تقوم عليه فيزياء الكم وكيمياء الكم ونظرية الحقل الكمومي وتقانة الكم وعلوم المعلومات الكمومية.
تُسمَّى مجموعة النظريات التي كانت موجودةً قبل ظهور ميكانيكا الكم الفيزياء الكلاسيكية، وهي تصف جوانبَ عديدةً من الطبيعة باعتماد مقياس عياني، ولكنها لا تصلح لوصف الظواهر الحاصلة في المقاييس الذرية ودون الذرية. يمكن اشتقاق معظم النظريات في الفيزياء الكلاسيكية من ميكانيكا الكم مثل تقريب صالح على نطاق واسع (عياني).[3]
تختلف ميكانيكا الكم (أو الحركة الكمومية) عن الفيزياء الكلاسيكية في اقتصار الطاقة والزخم والزخم الزاوي (عزم الدوران) والكميات الأخرى من نظام مقيد على القيم المنفصلة (التكميم)، وللأجسام فيها خصائص الجسيمات والموجات معًا (ازدواجية موجة جسيم)؛ وهناك حدود لمدى دقة التنبؤ بقيمة الكمية المادية قبل قياسها، بالنظر إلى مجموعةٍ كاملةٍ من الشروط الأولية (مبدأ اللايقين).
طُوِّرت ميكانيكا الكم تدريجيًا انطلاقًا من نظرياتٍ تشرح الملاحظات التي لا يمكن التوفيق بينها وبين الفيزياء الكلاسيكية، مثل حل ماكس بلانك لمشكلة إشعاع الجسم الأسود في عام 1900، والمطابقة بين الطاقة والتردد في ورقة ألبرت أينشتاين عام 1905 والتي فسرت التأثير الكهروضوئي.[4] أدت هذه المحاولات المبكرة لفهم الظواهر العيانية -والمعروفة الآن باسم «نظرية الكم القديمة»- إلى التطور الكامل لميكانيكا الكم في منتصف عشرينيات القرن الماضي بواسطة نيلز بور وإرفين شرودنغر وفيرنر هايزنبيرغ وماكس بورن وبول ديراك وآخرين. صيغت النظرية الحديثة في أشكال رياضية مختلفة طورت خصيصًا لذلك. يوفر كيان رياضي -هو أحد هذه الأشكال الرياضية، ويسمى دالة الموجة- معلوماتٍ -على شكل سعاتٍ احتماليةٍ- حول قياسات طاقة الجسيم، وزخمه، والخصائص الفيزيائية الأخرى التي قد يتسم بها.
نظرة عامة ومفاهيم رئيسة
تسمح ميكانيكا الكم بحساب خصائص الأنظمة الفيزيائية وسلوكها. وهي تطبق عادةً على الأنظمة المجهرية: كالجزيئات والذرات والجسيمات دون الذرية. وقد أُثبتت قدرتها على الاحتفاظ بالجزيئات المعقدة التي تحتوي على آلاف الذرات،[5] ولكن تطبيقها على البشر يثير مشكلاتٍ فلسفيةٍ، مثل صديق ويغنر، ويظل تطبيقها على الكون كله تخمينيًا.[6] تحقق العلماء من تنبؤات ميكانيكا الكم من خلال التجربة بدرجةٍ عاليةٍ من الدقة.[note 1]
تكمن السمة الرئيسة لميكانيكا الكم في عدم قدرتها على التنبؤ على وجه اليقين بما سيحدث، وتقديمها احتمالاتٍ عوضًا عن ذلك. يُحسَب الاحتمال رياضيًا بأخذ مربع القيمة المطلقة لعدد مركب، والمعروف باسم "سعة الاحتمال". يُعرف هذا باسم قاعدة بورن، والتي سميت على اسم الفيزيائي ماكس بورن. فمثلًا يمكن وصف جسيمٍ كميٍّ مثل الإلكترون بواسطة دالة موجية تربط كل نقطةٍ في الفضاء بسعةٍ احتمالية. إن تطبيق قاعدة بورن على هذه السعات يعطي دالة الكثافة الاحتمالية للموقع الذي سيوجد فيه الإلكترون عند إجراء تجربةٍ لتعيين مكانه، وهذا أفضل ما يمكن للنظرية أن تقدمه؛ فهي لا يمكنها تحديد موقع الإلكترون على وجه اليقين. وتربط معادلة شرودنغر مجموعة السعات الاحتمالية لموقع لإلكترون المتعلقة بلحظةٍ زمنيةٍ معينةٍ بمجموعة السعات الاحتمالية المتعلقة بلحظةٍ زمنيةٍ أخرى.
إحدى نتائج القواعد الرياضية لميكانيكا الكم هي المقايضة حول إمكانية التنبؤ بين الكمومات المختلفة القابلة للقياس. تشير الصيغة الأكثر شهرةَ لمبدأ اللايقين هذا إلى أنه -وبغض النظر عن كيفية تحضير الجسيم الكمي أو مدى دقة ترتيب التجارب عليه- فإن من المستحيل وجود تنبؤٍ دقيقٍ لقياس كلا موقعه وزخمه في الوقت نفسه.
تعد ظاهرة التداخل الكمي إحدى النتائج الأخرى للقواعد الرياضية لميكانيكا الكم، وهي غالبًا ما تتضَّح من خلال تجربة الشق المزدوج. في النسخة الأصلية من هذه التجربة يُضيء مصدر ضوءٍ متسقٍ -كشعاع ليزر مثلًا- صفيحةً مثقوبةً بشقين متوازيين، ويلاحظ الضوء الذي يمر عبر الشقين على شاشةٍ تقع خلف الصفيحة المثقوبة.[2]:1.1–1.8[7]:102–111 تتسبب الطبيعة الموجية للضوء في تداخل موجات الضوء التي تعبر الشقين، مما ينتج عنه نطاقات ساطعة ومظلمة على الشاشة؛ وهي نتيجة لا يمكن توقعها إذا كان الضوء يتكون من جسيماتٍ كلاسيكية.[7] ومع ذلك دائمًا ما يُمتص الضوء على الشاشة عند نقاطٍ منفصلةٍ كجسيماتٍ فرديةٍ بدلًا من موجاتٍ؛ ويَظهر نمط التداخل من خلال الكثافة المتغيرة لاصطدامات هذه الجسيمات على الشاشة. علاوةً على ذلك وَجدت نسخٌ لاحقة للتجربة تتضمن وضع كاشفاتٍ عند الشقوق أن كل فوتون مكتشَفٍ يمر من خلال شقٍّ واحدٍ (كما هو الحال مع الجسيم الكلاسيكي)، وليس عبر كلا الشقين (كما الحال بالنسبة للموجة).[7]:109[8][9] ومع ذلك فإن مثل هذه التجارب تظهر أن الجسيمات لا تشكل نمط التداخل إذا اكتشف المرء الشق الذي تمر من خلاله. عُثر على جسيماتٍ أخرى ذات مقاسٍ ذريٍّ -مثل الإلكترونات- تُظهر السلوك نفسه عند إطلاقها نحو شقٍّ مزدوج.[2] وهو السلوك الذي يُعرف بازدواجية موجة-جسيم.
تنبأت ميكانيكا الكم بظاهرةٍ أخرى غير بدهيّةٍ هي ظاهرة النفق الكمومي، وفيها يمكن للجسيم الذي يتقدم باتجاه حاجز جهدي أن يتخطاه ولو كانت طاقته الحركية أصغر من الحد الأقصى المحتمل.[10] بينما في الميكانيكا الكلاسيكية سيجري احتجاز هذا الجسيم. ثمة نتائج عديدة مهمة للنفق الكمي مرتبطة بالاضمحلال الإشعاعي، وبالاندماج النووي في النجوم، وتطبيقات مثل مجهر المسح النفقي وثنائي المساري النفقي.[11]
عندما تتفاعل الأنظمة الكمومية يمكن أن تكون النتيجة إنشاء تشابك كمي: فتصبح خصائصها متشابكةً لدرجة أن وصف الكل بالاعتماد على الأجزاء الفردية فقط لا يعود ممكنًا. دعا إرفين شرودنغر التشابكَ «... السمةَ المميزةَ لميكانيكا الكم التي تفرض خروجها بالكامل عن خطوط الفكر الكلاسيكية».[12] يتيح التشابك الكمي الخصائص غير البدهيّةِ للتخاطر الزائف الكمي، ويمكن أن يكون موردًا قيّمًا في بروتوكولات الاتصال، مثل توزيع المفاتيح الكمومية والترميز فائق الكثافة.[13] وعلى عكس الاعتقاد الخاطئ الشائع لا يسمح التشابك بإرسال إشاراتِ أسرع من الضوء، كما يتضح من نظرية عدم الاتصال.[13]
ثمة احتمال آخر ممكن ينتج عن التشابك الكمي هو اختبار «المتغيرات الخفية»، وهي خصائص افتراضية أكثر جوهريةً من الكمومات التي تتناولها نظرية الكم نفسها، ومن شأنها أن تسمح بتنبؤاتٍ أكثر دقةً مما توفره نظرية الكم. أظهرت مجموعة من النتائج -وأهمها مبرهنة بل- أن الفئات العريضة من نظريات المتغيرات الخفية هي في الواقع غير متوافقةٍ مع فيزياء الكم. وفقًا لمبرهنة بل إذا كانت الطبيعة تعمل بالفعل طبقًا لأي نظريةٍ لمتغيراتٍ محليةٍ خفيةٍ، فإن نتائج "اختبار بل" ستكون مقيَّدةً بطريقةٍ معينةٍ قابلةٍ للقياس الكمي. أجري العديد من اختبارات بل باستخدام جسيماتٍ متشابكةٍ، وقد أظهرت نتائجَ غير متوافقةٍ مع القيود التي تفرضها المتغيرات الخفية المحلية.[14][15]
من غير الممكن تقديم هذه المفاهيم بأكثرَ من طريقةٍ سطحيةٍ دون تقديم الرياضيات الفعلية المعنية؛ لا يتطلب فهم ميكانيكا الكم معالجة الأعداد المركبة فحسب، بل أيضًا الجبر الخطي والمعادلات التفاضلية ونظرية الزمر وموضوعاتٍ أخرى أكثر تقدمًا.[note 2] وفقًا لذلك ستقدم هذه المقالة صياغةً رياضيةً لميكانيكا الكم ومسحًا لتطبيقاتها على بعض الأمثلة المفيدة التي جرت دراستها كثيرًا.
صياغة رياضية
المقالة الرئيسة: صياغة رياضية لميكانيكا الكم
تكون حالة النظام الميكانيكي الكمومي في الصيغة الرياضية الدقيقة لميكانيكا الكم عبارةً عن متجه � ينتمي إلى فضاء هيلبرت العقدي (القابل للفصل) �
ينتمي إلى فضاء هيلبرت العقدي (القابل للفصل) � . يُفترض أن هذا المتجه يجري تطبيعه ضمن الجداء الداخلي لفضاء هيلبرت، أي إنه يخضع لـ⟨�,�⟩=1
. يُفترض أن هذا المتجه يجري تطبيعه ضمن الجداء الداخلي لفضاء هيلبرت، أي إنه يخضع لـ⟨�,�⟩=1 ، وهو محدد جيد حتى عدد معقد من المعامل 1 (المرحلة العامة)، أي �
، وهو محدد جيد حتى عدد معقد من المعامل 1 (المرحلة العامة)، أي � style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1028"> و����
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1028"> و���� style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle e^{i\alpha }\psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1029"> تمثل النظام الفعلي نفسه. بعبارةٍ أخرى الحالات المحتملة هي نقاط في الفضاء الإسقاطي لفضاء هيلبرت، والتي تسمى عادةً فضاء الإسقاط العقدي. تعتمد الطبيعة الدقيقة لفضاء هيلبرت على النظام؛ فعلى سبيل المثال لوصف الموقع والزخم، فإن فضاء هيلبرت هو فضاء الدوال العقدية القابلة للتكامل المربع �2(�)
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle e^{i\alpha }\psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1029"> تمثل النظام الفعلي نفسه. بعبارةٍ أخرى الحالات المحتملة هي نقاط في الفضاء الإسقاطي لفضاء هيلبرت، والتي تسمى عادةً فضاء الإسقاط العقدي. تعتمد الطبيعة الدقيقة لفضاء هيلبرت على النظام؛ فعلى سبيل المثال لوصف الموقع والزخم، فإن فضاء هيلبرت هو فضاء الدوال العقدية القابلة للتكامل المربع �2(�) style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle L^{2}(\mathbb {C} )}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1030">، بينما فضاء هلبرت لمغزل بروتون واحد هو ببساطة فضاء المتجهات العقدية ثنائية الأبعاد �2
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle L^{2}(\mathbb {C} )}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1030">، بينما فضاء هلبرت لمغزل بروتون واحد هو ببساطة فضاء المتجهات العقدية ثنائية الأبعاد �2 style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \mathbb {C} ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1031"> مع الجداء الداخلي المعتاد.
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \mathbb {C} ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1031"> مع الجداء الداخلي المعتاد.
يجري تمثيل الكمومات المادية ذات الأهمية -الموقع، والزخم، والطاقة، والمغزلية- بواسطة المراقبات، وهي مؤثرات خطية هيرميتية (بتعبيرٍ أدق مساعد ذاتي) تعمل في فضاء هيلبرت. يمكن أن تكون الحالة الكمومية متجهًا ذاتيًا يمكن ملاحظته، وفي هذه الحالة يطلق عليها اسم حالة ذاتية، وتتوافق القيمة الذاتية المرتبطة مع قيمة ما يمكن ملاحظته في تلك الحالة الذاتية. ستكون الحالة الكمومية مزيجًا خطيًا من حالاتٍ ذاتيةٍ عموماً، والمعروف باسم التراكب الكمومي. عندما يجري قياس ما يمكن ملاحظته، ستكون النتيجة واحدة من قيمها الذاتية مع الاحتمال الذي قدمته قاعدة بورن: في أبسط الحالات، تكون القيمة الذاتية � غير منهارةٍ ويجري إعطاء الاحتمال بواسطة |⟨�→,�⟩|2
غير منهارةٍ ويجري إعطاء الاحتمال بواسطة |⟨�→,�⟩|2 ، وفيه �→
، وفيه �→ هو المتجه الذاتي المرتبط به. تنهار القيمة الذاتية عادةً ويُعطى الاحتمال باستعمال ⟨�,���⟩
هو المتجه الذاتي المرتبط به. تنهار القيمة الذاتية عادةً ويُعطى الاحتمال باستعمال ⟨�,���⟩ ، وفيه ��
، وفيه �� هو الإسقاط على الفضاء الذاتي المرتبطة به. في الحالة المستمرة تعطي هذه الصيغ بدلاً من ذلك كثافة الاحتمال.
هو الإسقاط على الفضاء الذاتي المرتبطة به. في الحالة المستمرة تعطي هذه الصيغ بدلاً من ذلك كثافة الاحتمال.
إذا تُوُصِّلَ -بعد القياس- إلى النتيجة � فيُفترض أن الحالة الكمومية تنهار إلى �→
فيُفترض أن الحالة الكمومية تنهار إلى �→ ، في الحالة غير المنهارة أو ���/⟨�,���⟩
، في الحالة غير المنهارة أو ���/⟨�,���⟩ في الحالة العامة. وعليه فإن الطبيعة الاحتمالية لميكانيكا الكم تنبع من فعل القياس، وهو أحد أصعب جوانب الأنظمة الكمومية قابليةً للفهم، وقد كان الموضوع الرئيسي في مناظرات بور-أينيشتاين الشهيرة، حيث حاول فيها العالمان توضيح هذه المبادئ الرئيسة عن طريق التجارب الفكرية. وفي العقود التي تلت صياغة ميكانيكا الكم جرت دراسة مسألة ماهية «القياس» على نطاقٍ واسع، وصيغت تفسيرات جديدة لميكانيكا الكم تتخلص من مفهوم «انهيار الدالة الموجية» (انظر على سبيل المثال تفسير العوالم المتعددة). الفكرة الأساس هي أن دوال الموجة الخاصة بنظامٍ كميٍّ وجهاز قياسٍ تتشابك عندما يتفاعلان، وحينها يتوقف النظام الكمي الأصيل عن الوجود بصفته كيانًا مستقلًا. لمزيدٍ من التفاصيل راجع مقال القياس في ميكانيكا الكم.[18]
في الحالة العامة. وعليه فإن الطبيعة الاحتمالية لميكانيكا الكم تنبع من فعل القياس، وهو أحد أصعب جوانب الأنظمة الكمومية قابليةً للفهم، وقد كان الموضوع الرئيسي في مناظرات بور-أينيشتاين الشهيرة، حيث حاول فيها العالمان توضيح هذه المبادئ الرئيسة عن طريق التجارب الفكرية. وفي العقود التي تلت صياغة ميكانيكا الكم جرت دراسة مسألة ماهية «القياس» على نطاقٍ واسع، وصيغت تفسيرات جديدة لميكانيكا الكم تتخلص من مفهوم «انهيار الدالة الموجية» (انظر على سبيل المثال تفسير العوالم المتعددة). الفكرة الأساس هي أن دوال الموجة الخاصة بنظامٍ كميٍّ وجهاز قياسٍ تتشابك عندما يتفاعلان، وحينها يتوقف النظام الكمي الأصيل عن الوجود بصفته كيانًا مستقلًا. لمزيدٍ من التفاصيل راجع مقال القياس في ميكانيكا الكم.[18]
جرى وصف النمو الزمني للحالة الكمومية بواسطة معادلة شرودنغر:
�ℏ����(�)=��(�)
وتشير � فيها إلى هاملتوني يمكن ملاحظته المقابلة للطاقة الكلية للنظام، وℏ
فيها إلى هاملتوني يمكن ملاحظته المقابلة للطاقة الكلية للنظام، وℏ هو ثابت بلانك المختزَل. يُدخل الثابت �ℏ
هو ثابت بلانك المختزَل. يُدخل الثابت �ℏ لكي يقلل هاميلتوني إلى هاملتونيان الكلاسيكي في الحالات التي يُقرَّب فيها النظام الكمومي باستعمال النظام الكلاسيكي؛ وتسمى القدرة على إجراء مثل هذا التقريب في حدودٍ معينةٍ مبدأ التطابق.
لكي يقلل هاميلتوني إلى هاملتونيان الكلاسيكي في الحالات التي يُقرَّب فيها النظام الكمومي باستعمال النظام الكلاسيكي؛ وتسمى القدرة على إجراء مثل هذا التقريب في حدودٍ معينةٍ مبدأ التطابق.
يُعطى حل هذه المعادلة التفاضلية كما يأتي:
�(�)=�−���/ℏ�(0)
يُعرف عامل المؤثر �(�)=�−���/ℏ باسم عامل النمو الزمني ولديه الخاصة الحاسمة بأنه وحدوي. يعتبر النمو الزمني هذا حتميًا بمعنى أنه -بالنظر إلى حالةٍ كموميةٍ أوليةٍ �(0)
باسم عامل النمو الزمني ولديه الخاصة الحاسمة بأنه وحدوي. يعتبر النمو الزمني هذا حتميًا بمعنى أنه -بالنظر إلى حالةٍ كموميةٍ أوليةٍ �(0) - يقدم تنبؤًا محددًا لماهية الحالة الكمية �(�)
- يقدم تنبؤًا محددًا لماهية الحالة الكمية �(�) في أي وقت لاحق.[19]
في أي وقت لاحق.[19]
كثافات الاحتمالية المقابلة للدوال الموجية للإلكترون في ذرة الهيدروجين التي تمتلك مستويات طاقة محددة (تزداد من أعلى الصورة إلى الأسفل: ... ,n = 1, 2, 3) والعزم الزاوي (يزداد من اليسار إلى اليمين: ... ,s, p, d). تتوافق المناطق الأكثر كثافة مع كثافة احتمالية أعلى في قياس الموقع. يمكن مقارنة دوال الموجة هذه مباشرة بأرقام كلادني للأنماط الصوتية للاهتزاز في الفيزياء الكلاسيكية وهي أنماط من التذبذب أيضًا، تمتلك طاقة محددة وبالتالي ترددًا محددًا. يجري قياس الزخم الزاوي والطاقة ويأخذان قيمًا منفصلة فقط مثل تلك الموضحة (كما الحال بالنسبة للترددات الرنانة في الصوتيات).
من خلال دوال الموجة «المتزنة». على سبيل المثال يُصوَّر إلكترون واحد في ذرة غير مستثارةٍ تصويراً تقليدياً على هيئة جسيمٍ متحرِّكٍ في مسارٍ دائريٍّ حول النواة الذرية، بينما يجري وصفه في ميكانيكا الكم بواسطة دالة موجةٍ متزنةٍ تحيط بالنواة. مثلًا دالة الموجة الإلكترونية لذرة هيدروجينٍ غير مستثارةٍ هي دالة متناظرة كرويًا تُعرف باسم مدار s (الشكل 1).
تُعرف الحلول التحليلية لمعادلة شرودنغر بعددٍ قليلٍ جدًا من النماذج البسيطة نسبيًا من أتباع هاميلتونيين بما في ذلك الهزاز التوافقي الكمومي والجسيم في الصندوق وكاتيون ثنائي الهيدروجين وذرة الهيدروجين. حتى ذرة الهليوم -التي تحتوي على إلكترونين فقط- تحدت جميع المحاولات في علاجٍ تحليليٍّ كامل.
ومع هذا ثمة تقانات لإيجاد حلولٍ تقريبية. تستخدم إحدى الطرق -المسماة نظرية الاضطراب- النتيجة التحليلية لنموذجٍ ميكانيكيٍّ كميٍّ بسيطٍ لإنشاء نتيجةٍ لنموذجٍ ذي صلةٍ، ولكنه أكثر تعقيدًا -على سبيل المثال- عن طريق إضافة طاقةٍ كامنةٍ ضعيفة. هناك طريقة أخرى تسمى «معادلة الحركة شبه الكلاسيكية»، والتي تنطبق على الأنظمة التي ينتج عنها ميكانيكا الكم انحرافات صغيرة فقط عن السلوك الكلاسيكي. يمكن بعد ذلك حساب هذه الانحرافات بناءً على الحركة الكلاسيكية. هذا النهج مهم خصوصاً في حقل الفوضى الكمومية.
مبدأ اللايقين
إحدى النتائج الرئيسة للصيغ الكمومية هي مبدأ اللايقين. ينص هذا المبدأ في أكثر أشكاله شيوعًا على أنه لا يوجد تحضير لجسيمٍ كميٍّ يمكن أن يشير ضمنًا إلى تنبؤاتٍ دقيقةٍ في الوقت نفسه لتحديد موقعه وقياس زخمه.[20][21] كل من الموقع والزخم يمكن ملاحظتهما، مما يعني أنهما ممثَّلان من قبل المؤثرات الهيريميتية. مؤثر الموقع �^ ومؤثر الزخم �^
ومؤثر الزخم �^ لا يستبدان بل يلبيان علاقة التبديل القانوني:
لا يستبدان بل يلبيان علاقة التبديل القانوني:
[�^,�^]=�ℏ![{\displaystyle [{\hat {X}},{\hat {P}}]=i\hbar }](http:///C:\Users\qcer\AppData\Local\Temp\msohtmlclip1\01\clip_image001.gif)
وبالنظر إلى الحالة الكمومية تتيح لنا قاعدة بورن حساب قيم التوقع لكل من � و�
و� ، بالإضافة إلى قوى كل منهما. تحديد اللايقين للملاحظة من خلال الانحراف المعياري، لدينا
، بالإضافة إلى قوى كل منهما. تحديد اللايقين للملاحظة من خلال الانحراف المعياري، لدينا
��=⟨�2⟩−⟨�⟩2
وبالمثل بالنسبة للزخم:
��=⟨�2⟩−⟨�⟩2 alt="{\displaystyle \sigma _{P}={\sqrt {\langle {P}^{2}\rangle -\langle {P}\rangle ^{2}}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1054">
alt="{\displaystyle \sigma _{P}={\sqrt {\langle {P}^{2}\rangle -\langle {P}\rangle ^{2}}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1054">
ينص مبدأ اللايقين على ذلك
����≥ℏ2 ' alt="{\displaystyle \sigma _{X}\sigma _{P}\geq {\frac {\hbar }{2}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1055">
' alt="{\displaystyle \sigma _{X}\sigma _{P}\geq {\frac {\hbar }{2}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1055">
يمكن نظرياً أن يكون أي من الانحرافين المعياريين ذا قيمةٍ صغيرةٍ عشوائيًّا، ولكن ليس كلاهما في وقتٍ واحد.[22] تُعمَّم هذه المتباينة على أزواجٍ عشوائيةٍ من المؤثرات المترابطة ذاتيًا � alt="{\displaystyle A}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1056"> و�
alt="{\displaystyle A}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1056"> و� . المبدل لهذين الموثرين هو
. المبدل لهذين الموثرين هو
[�,�]=��−�� ' alt="{\displaystyle [A,B]=AB-BA}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1058">
' alt="{\displaystyle [A,B]=AB-BA}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1058">
وهذا يوفر الحد الأدنى لجداء الانحرافات المعيارية:
����≥12|⟨[�,�]⟩|![{\displaystyle \sigma _{A}\sigma _{B}\geq {\frac {1}{2}}\left|\langle [A,B]\rangle \right|}](http:///C:\Users\qcer\AppData\Local\Temp\msohtmlclip1\01\clip_image001.gif)
ثمة نتيجة أخرى لعلاقة التبديل القانوني وهي أن مؤثري الموقع والزخم عبارة عن تحويلات فورييه لبعضهم بعضَا، فيكون وصف كائنٍ وفقًا لزخمه الخاص به هو تحويل فورييه لوصفه وفقًا لموقعه. وحقيقةً إن الاعتماد في الزخم هو تحويل فورييه للاعتماد في الموقع يعني أن مؤثر الزخم مكافئ (حتى عامل �/ℏ ) لأخذ المشتق وفقًا للموقع، لأن التمايز في تحليل فورييه يتوافق مع الضرب في الفضاء المزدوج، وهو السبب في المعادلات الكمومية في فضاء الموقع، يستبدل الزخم ��
) لأخذ المشتق وفقًا للموقع، لأن التمايز في تحليل فورييه يتوافق مع الضرب في الفضاء المزدوج، وهو السبب في المعادلات الكمومية في فضاء الموقع، يستبدل الزخم �� بـ−�ℏ∂∂�
بـ−�ℏ∂∂� alt="{\displaystyle -i\hbar {\frac {\partial }{\partial x}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1062">، وعلى وجه الخصوص في معادلة شرودنغر غير النسبية في فضاء الموقع، يستبدل مصطلح مربع الزخم بضرب لابلاسيه −ℏ2
alt="{\displaystyle -i\hbar {\frac {\partial }{\partial x}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1062">، وعلى وجه الخصوص في معادلة شرودنغر غير النسبية في فضاء الموقع، يستبدل مصطلح مربع الزخم بضرب لابلاسيه −ℏ2 ' alt="{\displaystyle -\hbar ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1063"> .[20]
' alt="{\displaystyle -\hbar ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1063"> .[20]
الأنظمة المركبة والتشابك
عندما ينظر إلى نظامين كموميين مختلفين معًا، فإن فضاء هيلبرت للنظام المدمج هو ناتج جداء الموتر لفضاءات هيلبرت للمكونين. مثلًا لنفترض أن A وB نظامان كموميان مع فضاءات هيلبرت �� alt="{\displaystyle {\mathcal {H}}_{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1064"> و��
alt="{\displaystyle {\mathcal {H}}_{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1064"> و�� alt="{\displaystyle {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1065"> على التوالي. إذن فضاء هيلبرت للنظام المركب هو
alt="{\displaystyle {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1065"> على التوالي. إذن فضاء هيلبرت للنظام المركب هو
���=��⊗�� alt="{\displaystyle {\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1066">
alt="{\displaystyle {\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1066">
إذا كانت حالة النظام الأول هي المتجه �� alt="{\displaystyle \psi _{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1067"> وكانت حالة النظام الثاني هي ��
alt="{\displaystyle \psi _{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1067"> وكانت حالة النظام الثاني هي �� alt="{\displaystyle \psi _{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1068">، فإن حالة النظام المركب هي
alt="{\displaystyle \psi _{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1068">، فإن حالة النظام المركب هي
��⊗��
لا يمكن كتابة جميع الحالات في فضاء هيلبرت المشترك ��� بهذا الشكل، لأن مبدأ التراكب يشير إلى أن التوليفات الخطية لهذه الحالات «القابلة للفصل» أو «حالات المنتج» صالحة أيضًا. على سبيل المثال إذا كانت كلتا ��
بهذا الشكل، لأن مبدأ التراكب يشير إلى أن التوليفات الخطية لهذه الحالات «القابلة للفصل» أو «حالات المنتج» صالحة أيضًا. على سبيل المثال إذا كانت كلتا �� و��
و�� حالتان ممكنتان للنظام �
حالتان ممكنتان للنظام � وبالمثل ��
وبالمثل �� و��
و�� كلتاهما حالتان ممكنتان للنظام �
كلتاهما حالتان ممكنتان للنظام � إذن
إذن
12(��⊗��+��⊗��)
هي حالة مشتركة صالحة لا يمكن فصلها، والحالات غير القابلة للفصل تسمى متشابكة.[23][24]
إذا كانت حالة النظام المركب متشابكةً فمن المستحيل وصف أي نظام مكون A أو النظام B بواسطة متجه الحالة. يمكن للمرء بدلاً من ذلك تحديد مصفوفات الكثافة المنخفضة التي تصف الإحصائيات التي يمكن الحصول عليها من خلال إجراء قياساتٍ على أي نظامٍ مكونٍ بمفرده. يؤدي هذا بالضرورة إلى فقدان المعلومات، على الرغم من أن معرفة مصفوفات الكثافة المنخفضة للأنظمة الفردية لا يكفي لإعادة بناء حالة النظام المركب.[23][24] تمامًا كما تحدد مصفوفات الكثافة حالة نظامٍ فرعيٍّ لنظامٍ أكبر. بالمقابل تصف (POVMs) التأثير على نظام فرعي للقياس الذي يجري على نظام أكبر. تستخدم POVM على نطاق واسع في نظرية المعلومات الكمومية.[23][25]
وكما هو موضح أعلاه يعد التشابك سمة رئيسة لنماذج عمليات القياس التي تتشابك فيها الأدوات مع النظام الذي يجري قياسه. تتفاعل الأنظمة متشابكة مع البيئة حيث توجد، وهي ظاهرة تُعرف باسم إزالة الترابط الكمي. هذا يمكن أن يفسر لماذا -من الناحية العملية- تصعب ملاحظة التأثيرات الكمية في الأنظمة الأكبر من المجهرية.[26]
التكافؤ بين الصيغ
توجد صيغ عديدة متكافئة رياضيًا لوصف ميكانيكا الكم، أقدمها وأشهرها هي «نظرية التحويل» التي اقترحها بول ديراك، والتي توحد وتعمم الصيغتين الأقدم لميكانيكا الكم؛ ميكانيكا المصفوفة (وضعها فيرنر هايزنبيرغ) وميكانيكا الموجات (وضعها إرفين شرودنغر).[27] الصيغة البديلة لميكانيكا الكم هي صيغة فاينمان لتكامل المسار، وفيها يُنظر إلى السعة الميكانيكية الكمومية بوصفها مجموعاً للمسارات التقليدية وغير التقليدية الممكنة بين الوضعين الابتدائي والنهائي. هذا هو المقابل الميكانيكي الكمومي لمبدأ الفعل في الميكانيكا التقليدية.
التناظرات وقوانين الحفظ
المقالة الرئيسة: مبرهنة نويثر
يُعرف هاميلتونيان � بأنه مُولِّد نمو الوقت، لأنه يحدد عامل النمو الزمني الوحدوي �(�)=�−���/ℏ
بأنه مُولِّد نمو الوقت، لأنه يحدد عامل النمو الزمني الوحدوي �(�)=�−���/ℏ لكل قيمة من قيم �
لكل قيمة من قيم � . يترتب على هذه العلاقة بين �(�)
. يترتب على هذه العلاقة بين �(�) و�
و� حفظ �
حفظ � ويمكن ملاحظته أن توقُّع �
ويمكن ملاحظته أن توقُّع � : لن يُغير القيمة بمرور الوقت. تُعمم هذه العبارة رياضيًا أي عامل هرميتي �
: لن يُغير القيمة بمرور الوقت. تُعمم هذه العبارة رياضيًا أي عامل هرميتي � يمكن أن يولد مجموعةً من العوامل الوحدوية ذات معلماتٍ بواسطة متغير �
يمكن أن يولد مجموعةً من العوامل الوحدوية ذات معلماتٍ بواسطة متغير � . في ظل التطور الناتج عن �
. في ظل التطور الناتج عن � ، سيجري حفظ أي �
، سيجري حفظ أي � يمكن ملاحظته ويتنقل مع �
يمكن ملاحظته ويتنقل مع � . علاوةً على ذلك إذا كان �
. علاوةً على ذلك إذا كان � محفوظًا بالنمو تحت �
محفوظًا بالنمو تحت � ، فإن �
، فإن � يجري حفظه في ظل النمو الناتج عن �
يجري حفظه في ظل النمو الناتج عن � . يشير هذا إلى نسخةٍ كميةٍ للنتيجة التي أثبتتها إيمي نويثر في الميكانيكا الكلاسيكية (لاغرانج): لكل تناظرٍ قابلٍ للاشتقاق الهاملتوني يوجد قانون حفظ مطابق
. يشير هذا إلى نسخةٍ كميةٍ للنتيجة التي أثبتتها إيمي نويثر في الميكانيكا الكلاسيكية (لاغرانج): لكل تناظرٍ قابلٍ للاشتقاق الهاملتوني يوجد قانون حفظ مطابق
تقول النظرية الجديدة إنه قد يكون هناك "كون آخر مضاد"، يعود إلى الوراء في الزمن قبل الانفجار العظيم.
وتفترض النظرية أن الكون المبكر كان صغيرًا وساخنًا وكثيفًا ومنتظمًا لدرجة أن الوقت يبدو متماثلًا بالتقدم للأمام وللخلف. وإذا كان هذا صحيحًا ، فإن النظرية الجديدة تعني أن المادة المظلمة ليست غامضة جدًا، وإنها مجرد ظل جديدة لجسيم شبحي يسمى "نيوترينو" لا يمكن أن يوجد إلا في هذا النوع من الكون
وتشير النظرية إلى أنه لن تكون هناك حاجة لفترة "تضخم" توسعت بسرعة في حجم الكون الشاب بعد فترة وجيزة من الانفجار العظيم. إذا كان هذا صحيحًا، فإن التجارب المستقبلية للبحث عن موجات الجاذبية، أو لتحديد كتلة النيوترينوات، يمكن أن تجيب بشكل نهائي عما إذا كان هذا الكون المرآة المضاد موجودًا.
حدد الفيزيائيون مجموعة من التناظرات الأساسية في الطبيعة. أهم ثلاثة تناظرات هي: الشحنة (إذا قلبت شحنات جميع الجسيمات المشاركة في تفاعل مع الشحنة المعاكسة ، فستحصل على نفس التفاعل)، التكافؤ (إذا نظرت إلى الصورة المتطابقة للتفاعل ، تحصل على نفس النتيجة)، والوقت (إذا قمت بتشغيل تفاعل إلى الوراء في الوقت المناسب ، فسيبدو هو نفسه).
تخضع التفاعلات الفيزيائية لمعظم هذه التناظرات في معظم الأوقات، مما يعني أنه توجد أحيانًا انتهاكات. لكن الفيزيائيين لم يلاحظوا أبدًا انتهاكًا لمجموعة من التماثلات الثلاثة في نفس الوقت. إذا أخذت كل تفاعل لوحظ في الطبيعة وقلبت الشحنات ، وأخذت صورة معكوسة ، وقمت بتشغيلها للخلف في الوقت المناسب ، فإن هذه التفاعلات تتصرف تمامًا.
يتم إعطاء هذا التناظر الأساسي اسمًا: تناظر CPT ، للشحنة (C) ، التكافؤ (P) والوقت (T).
وفي دراسة بحثية جديدة تم قبولها مؤخرًا للنشر في مجلة حوليات الفيزياء، اقترح العلماء توسيع هذا التناظر المشترك. عادةً ما ينطبق هذا التناظر فقط على التفاعلات - القوى والمجالات التي تشكل فيزياء الكون. لكن ربما، إذا كان هذا التناظر مهما للغاية، فإنه ينطبق على الكون بأكمله نفسه.
بعبارة أخرى، تمتد هذه الفكرة من هذا التناظر من مجرد تطبيق على "الجهات الفاعلة" في الكون (القوى والحقول) إلى "المرحلة" نفسها ، الشيء المادي الكامل للكون. خلق المادة المظلمة نحن نعيش في عالم يتسع.
هذا الكون مليء بالعديد من الجسيمات التي تقوم بالكثير من الأشياء المثيرة للاهتمام ، وتطور الكون يتحرك إلى الأمام بمرور الوقت. إذا قمنا بتوسيع مفهوم تناظر CPT ليشمل الكون بأكمله ، فإن نظرتنا للكون لا يمكن أن تكون الصورة الكاملة. بدلا من ذلك ، يجب أن يكون هناك المزيد. للحفاظ على تناظر CPT في جميع أنحاء الكون ، يجب أن يكون هناك كوزموس صورة معكوسة يوازن بيننا. سيكون لهذا الكون جميع الشحنات المعاكسة أكثر مما لدينا ، وينقلب في المرآة ، ويعود إلى الوراء في الوقت المناسب. كوننا مجرد توأم. مجتمعة ، يطيع الكونان تناظر CPT.
ووجد الباحثون أن الشروط المفروضة من خلال الانصياع لتناظر CPT سوف تملأ كوننا بالنيوترينوات اليمنى، وهو ما يكفي لتفسير المادة المظلمة.
تنبؤات في المرآة
لن نتمكن من الوصول إلى توأمنا، لأنه موجود "خلف" الانفجار العظيم ، قبل بداية كوننا. لكن هذا لا يعني أنه لا يمكننا اختبار هذه الفكرة.
وجد الباحثون بعض النتائج الملاحظة لهذه الفكرة. على سبيل المثال ، توقعوا أن أنواع النيوترينو الثلاثة المعروفة يجب أن تكون جميعها جسيمات ماجورانا، مما يعني أن جزيئاتها المضادة (على عكس الجسيمات العادية مثل الإلكترون، التي لها نظائر من المادة المضادة تسمى البوزيترونات). حتى الآن، علماء الفيزياء ليسوا متأكدين مما إذا كانت النيوترينوات تمتلك هذه الخاصية أم لا.
بالإضافة إلى ذلك ، توقعوا أن يكون أحد أنواع النيوترينو عديم الكتلة. في الوقت الحالي ، يمكن للفيزيائيين فقط وضع حدود عليا لكتل النيوترينو. إذا تمكن الفيزيائيون من قياس كتل النيوترينو بشكل قاطع ، وكان أحدهم عديم الكتلة بالفعل ، فإن ذلك سيعزز بشكل كبير فكرة الكون المتماثل CPT.
أما الزمن فتعريفه قد يكون صعبا ولكن يقال أنالزمن هو عملية تقدم الأحداث بشكلٍ مستمر وإلى أجل غير مسمى بدءًا من الماضي مروراً بالحاضر وحتى المستقبل، وهي عملية لا رجعة فيها/متعذر إلغاؤها.[1][2][3] ربما يكون مصطلح الزمن الأعصى على التعريف، فالزمن أمر نحس به أو نقيسه أو نقوم بتخمينه، وهو يختلف باختلاف وجهة النظر التي ننظر بها بحيث يمكننا الحديث عن زمن نفسي أو زمن فيزيائي أو زمن تخيلي.
لكن يمكننا حصر الزمن مبدئيًا بالإحساس الجماعي للناس كافة على توالي الأحداث بشكل لا رجوع فيه، هذا التوالي الذي يتجلى أكثر ما يتجلى بتوالي الليل والنهار وتعاقب الأيام فرض على الناس تخيل الزمن بشكل نهر جار باتجاه محدد لا عودة فيه.
مع الأيام لاحظ البشر أن العديد من الظواهر الفيزيائية بدءًا من حركات الشمس إلى تساقط الرمل من وعاء زجاجي إلى اهتزاز نوّاس بسيط تأخذ فترات زمنية متساوية حسب تقديرهم مما دفعهم لتطوير ميقاتيات وأدوات لقياس الزمن باستخدام هذه الظواهر فأوجدوا المزولة الشمسية ثم الساعة الرملية ثم ساعة النواس أو البندول.
وفي كل هذه الأزمان تم اعتبار الزمن على أنه أحد المطلقات فالفترات الزمنية الفاصلة بين حدثين مختلفين ثابت بالنسبة لكافة المراقبين، وهذا أمر حافظ عليه نيوتن باعتباره الزمن شيئا مطلقا كونيا فتغيرات الزمن ثابتة في جميع أنحاء الكون، وهو يجري أبدًا كما هو بالنسبة لجملة فيزيائية تتحرك بانتظام أو بتسارع، تتحرك حركة دائرية أو مستقيمة.
ما زال هذا المفهوم للزمن منتشرًا بين الناس كونه يطابق كثيرًا إحساسهم به إلا أن الفيزياء الحديثة قامت بإنزال الزمن عن عرشه وإلغاء صفة الإطلاق التي اتصف بها عبر السنين، فنظرية النسبية الخاصة اعتبرته أحد مكونات المسرح الكوني التي تجري فيه الأحداث وبالتالي أصبحت لكل جملة فيزيائية زمنها الخاص بها الذي يختلف عن زمن جملة فيزيائية أخرى.
قياس الزمن والتاريخ
بصورة عامة، أخذت طرق قياس الزمن صورتين منفصلتين: التقويم وهو أداة رياضية لتنظيم الفترات الزمنية، والساعة وهي آلة ميكانيكية تقيس مرور الوقت.[4] في الحياة اليومية، يتم الرجوع إلى الساعة في الفترات أقل من يوم بينما يتم الرجوع إلى التقويم في الفترات الأطول من يوم. بصورة متزايدة، تُظهر الأجهزة الكهربائية الشخصية كلا من التقويم والساعة في نفس الوقت.
تاريخ التقويم
تقترح الآثار من العصر الحجري القديم أن القمر كان يُستخدم في تقدير الوقت لأكثر من 6000 سنة. كان التقويم القمري من أول التقويمات ظهوراً حيث يتكون من 12 أو 13 شهرا قمريا (354 أو 384 يوما).[5] بدون ضبط التاريخ بطريقة الإقحام لإضافة أيام أو شهور لبعض السنوات، تنحرف الفصول سريعاً في تقويم مبني فقط على اثني عشر شهراً قمرياً. في التقويم الشمسي القمري شهرا إضافيا يُضاف لبعض السنوات للتعويض عن الفرق بين السنة الكاملة (المعروفة الآن بأنها حوالي 365.24 يوما) وبين سنة من اثني عشر شهرا قمريا. ظهرت الأرقام اثنا عشر وثلاثة عشر للتمييز في الكثير من الثقافات، جزئيا على الأقل بسبب هذه العلاقة بين الشهور والسنوات. ظهرت صور مبكرة أخرى للتقويم في أمريكا الوسطى، وخاصة في حضارة المايا القديمة. كان هذا التقويم دينيا فلكيا به 18 شهر في السنة و20 يوما في الشهر بالإضافة إلى خمسة أيام إضافية في نهاية كل عام.[6]
وضعت إصلاحات يوليوس قيصر في 45 ق.م الإمبراطورية الرومانية على تقويم شمسي. كان هذا التقويم اليولياني خاطئا حيث أن إقحامه كان لا يزال يسمح للانقلاب الشمسي والاعتدال الشمسي بالتقدم عكسه بحوالي 11 دقيقة في السنة. قدم البابا غريغوريوس الثالث عشر تصحيحا في 1582، وبدأت دول متعددة اعتماد التقويم الميلادي على مدار عدة قرون، ولكنه الآن أكثر تقويم مستخدم حول العالم بفارق كبير.
أثناء الثورة الفرنسية، تم اقتراح ساعة وتقويم جدد في محاولة لإعادة الوقت إلى المسيحية وخلق نظام أكثر عقلانية من أجل استبدال التقويم الميلادي. تكونت أيام التقويم الجمهوري الفرنسي من عشر ساعات في كل منها مائة دقيقة في كل منها مائة ثانية، مما يعتبر انحرافاً عن نظام العد الاثني عشري المستخدم في العديد من الثقافات الأخرى. تم إلغاء النظام لاحقا في سنة 1806.[7]
تاريخ آلات قياس الوقت
مزولة أفقية في تاغانروغ. ساعة رملية
تم اختراع عدد كبير من أجهزة القياس بهدف قياس الوقت. يُطلق على دراسة هذه الأجهزة اسم علم البنكامات.[8]
يعود جهاز مصري إلى حوالي 1500 ق.م –شبيه بالمسطرة حرف تي- والذي كان يقيس مرور الوقت باستخدام الظل الساقط من العمود الموجود على مسطرة غير خطية. كان حرف تي يوضع شرقا في الصباح، وعند الظهر يُقلب الجهاز ليتمكن من إسقاط ظله في اتجاه المساء.[9]
تستخدم المزولة قياسا يلقي بظله على عدد من العلامات التي تمثل الساعة. يحدد مكان سقوط الظل الساعة في المنطقة الزمنية. تعود فكرة تقسيم اليوم إلى أجزاء أصغر إلى المصريين بسبب اختراعهم المزولة والتي كانت تعمل على نظام اثني عشري. ترجع أهمية الرقم اثني عشر إلى عدد الدورات القمرية في السنة وعدد النجوم المستخدمة لحساب مرور الوقت ليلا.[10]
كانت أكثر أجهزة العالم القديم دقة في قياس الوقت هي الساعة المائية والتي وُجدت واحدة منها في مقبرة الفرعون المصري أمنحتب الأول. كانت الساعة المائية تُستخدم في قياس الساعات حتى في الليل ولكنها كانت تتطلب ضبطا يدويا لاستكمال تدفق الماء. حافظ اليونانيون القدماء وشعوب كلدو (جنوب بلاد ما بين النهرين) على قيسهم للوقت كجزء أساسي في ملاحظاتهم الفلكية. قدم المخترعون والمهندسون العرب تحسينات على استخدام الساعات المائية حتى العصور الوسطى. في القرن الحادي عشر، اخترع المخترعون والمهندسون الصينيون أول ساعة ميكانيكة مبنية على آلية ميزان الساعة.
تستخدم الساعة الرملية سريان الرمل لقياس مرور الوقت. استُخدمت هذه الساعات في الملاحة. استخدم فرناندو ماجلان 18 ساعة رملية على كل سفينة عند إبحاره حول الكرة الأرضية في 1522.
كانت أعواد البخور والشمع تُستخدم لقياس الوقت في المعابد والكنائس حول العالم. كانت ساعات الماء ولاحقا الساعات الميكانيكية تُستخدم لتحديد أحداث الكنائس والأديرة في العصور الوسطى.[11] بنى ريتشارد من والينجفورد (1292-1336) ساعة ميكانيكة شهيرة كآلة فلكية في حوالي 1330.
قدم غاليليو غاليلي إسهامات ضخمة في قياس الزمن بدقة، وخاصة كريستيان هوغنس مع اختراع الساعات القائمة على البندول مع اختراع جوست بورغي لعقرب الدقائق.[12]
تأتي الكلمة الإنجليزية clock والتي تعني الساعة من الكلمة الهولندية الوسطى klocke والتي تأتي بدورها من الكلمة اللاتينية الوسطى clocca والتي أتت في آخر الأمر من اللغة الكلتية والتي تشبه الكلمات الفرنسية واللاتينية والألمانية والتي تعني الجرس. تحدد مرور الساعات في البحر بواسطة الأجراس والتي كانت تدلل على الوقت (انظر جرس سفينة). تحددت الساعات في الكنائس عن طريق الأجراس مثل البحر.
تمتد الساعات من ساعات اليد إلى الأنواع الأخرى الأكثر غرابة من الساعات. تعمل الساعات على العديد من الوسائل بما في ذلك الجاذبية والنوابض والعديد من صور القوى الكهربية، كما يضبطها العديد من الوسائل الأخرى مثل الرقاص أو البندول.[13][14]
ظهرت المنبهات لأول مرة في اليونان القديمة حوالي سنة 250 ق.م في ساعة مائية تطلق صافرة. عدل كل من ليفي هتشنز وسيث توماس لاحقا على هذه الفكرة.
الكرونومتر هو أداة محمولة لتتبع الوقت والذي لا بد أن يصل إلى بعض أسس الدقة. في البداية، استُخدم المصطلح للإشارة إلى الكرونومتر البحري وهو أداة زمنية تستخدم لتحديد الطول الجغرافي باستخدام طرق الملاحة الفلكية، والتي كان جون هاريسون أول من حقق الدقة من خلالها. حديثا، تم تطبيق المصطلح أيضا على الكرونومتر الخاص بالزمن، وهي ساعة تصل إلى بعض أسس الدقة التي تضعها الشركة السويسرية COSC.
أكثر الآلات الزمنية دقة في تتبع الوقت هي الساعة الذرية،[15] والتي تبلغ دقتها ثانية كل عدة ملايين من السنين، وتستخدم في ضبط الساعات والآلات الزمنية الأخرى.
تستخدم الساعات الذرية الانتقالات الإلكترونية في بعض الذرات لقياس الثانية. أحد أكثر الذرات المستخدمة هي ذرة عنصر السيزيوم،[16] حيث تفحص معظم الساعات الذرية الحديثة السيزيوم بموجات الراديو لتحدد تردد اهتزازات هذه الإلكترونات. منذ 1967، حددت المنظمة الدولية للقياسات وحدة الزمن (الثانية) بناء على خواص ذرات السيزيوم. يعرف نظام الوحدات الدولي الثانية بأنها 9,192,631,770 دورة للإشعاع المقابل للانتقال بين مستويي طاقة للإلكترون من الحالة الأرضية لذرة السيزيوم.
اليوم يمكن استخدام نظام التموضع العالمي بالتنسيق مع بروتوكول وقت الشبكة لتوقيت وتزامن أنظمة قياس الوقت حول العالم.
في الكتابات الفلسفية من العصور الوسطى، كانت الذرة هي وحدة قياس الزمن حيث كان يُشار إليها بأنها أصغر وحدة ممكنة من الزمن. أول ذكر للكلمة في الإنجليزية في كتابات بيرثفيرث (كتاب علمي) في حوالي 1010-1012 حيث عرفها بأنها 1/564 من فترة الزخم (دقيقة ونصف) وبالتالي يساوي 15/94 من الثانية.[17]
منذ مايو 2010، أصبحت أصغر وحدات تقسيم الزمن هو الأس 12 للأتوثانية (1.2 × 10−17 ثانية) وهي حوالي 3.7 × 1026 من زمن بلانك.[18]
وحدات الزمن
الثانية هي الوحدة الأساسية لنظام الوحدات الدولي. الدقيقة هي 60 ثانية، والساعة تبلغ 60 دقيقة. يبلغ اليوم 24 ساعة أو 86,400 ثانية.
الدين
الزمن الخطي والزمن الدوري
كان للعديد من الحضارات القديمة مفهوم عجلة الزمن مثل الإنكا والمايا والهوبي والقبائل الأخرى في أمريكا الوسطى، بالإضافة إلى البابليين واليونانيين القدماء والهندوسيين والبوذيين والجاينيين وغيرهم، حيث اعتبروا الزمن على أنه تعاقب دوري ومتجانس ويتكون من أعمار متكررة تحدث لكل كائن حي في الكون ما بين مولده ووفاته.[19]
بشكل عام، يعتبر التراث الإسلامي والتراث اليهودي المسيحي أن الزمن يسير بصورة خطية واتجاه نسبي، حيث بدأ بفعل الخلق بواسطة الله. يرى التراث المسيحي التقليدي أن الزمن ينتهي (لاهوتيا) مع الإسخاتولوجيا المسيحية ونهاية النظام الحالي للأشياء أو ما يُعرف باسم «نهاية الزمان». في العهد القديم كتاب سفر الجامعة والمنسوب تقليديا إلى سليمان (970-928 ق.م)، اعتُبر الزمن (أو الكلمة العبرية זמן)وسيلة لإنفاذ أحداث القدر.[20]
الزمن في الميثولوجيا اليونانية
تفرق اللغة اليونانية بين مبدأين منفصلين: خرونوس وكايروس. يشير الأول إلى الزمن العددي أو التقويمي، بينما يشير الأخير (حرفيا اللحظة الحالية) إلى الزمن الإلهي أو الميتافيزيقي. في اللاهوت، كايروس قابل للتعداد على عكس خرونوس.
في الميثولوجيا اليونانية، كرونوس (باليونانية القديمة: Χρόνος) هو تشخيص الزمن. اسمه في اليونانية يعني «الزمن». عادة ما كان يتم تشخيص الزمن على أنه رجل عجوز حكيم له لحية طويلة رمادية.
الزمن في القبالة
طبقا للقبالة اليهودية، فالزمن مفارقة[21] ووهم،[22] فكل من المستقبل والماضي هي أحداث حاضرة مجمعة.
الفلسفة
"الزمن ليس مفهوما تجريبيا، فلا يمكننا تصور التواجد أو التتابع إن لم يوجد مفهوم الزمن كبديهة أساسية. بدون هذا الافتراض المسبق لن يكون بإمكاننا التمثيل لأنفسنا أن هناك أشياء تتواجد معا وفي نفس الوقت، أو في أوقات مختلفة، بعبارة أخرى متعاصرة أم متتالية".
“
”
إيمانويل كانت، نقد العقل المحض.
ينقسم الفلاسفة إلى رأيين متضادين بخصوص الزمن. أحد الرأيين هو جزء من التركيب الأساسي للفضاء الكوني أو بُعد مستقل عن الأحداث والذي تحدث فيه الأحداث متتالية. كان إسحق نيوتن أحد مناصري هذا الرأي الواقعي، ومن هنا أصبح يُشار إلي ذلك الرأي باسم الزمن النيوتوني.[23][24] الرأي المقابل هو أن الزمن لا يشير إلى أي نوع من «الاحتواء» والذي «تتحرك» الأشياء والأحداث خلاله، ولكنه جزء من بناء عقلي أساسي (مع المكان والعدد) والذي تحدث فيه أفعال وأحداث البشر. يرى هذا الرأي الثاني (مثل غوتفريد لايبنتس وإيمانويل كانت[25]) أن الزمن ليس بحدث أو شيء، وبالتالي فهو غير قابل للقياس في حد ذاته كما لا يمكن السفر عبره.[26]
علاوة على ذلك، ربما يكون هناك مكون ذاتي للزمن ولكن سواء لا تزال إمكانية الإحساس بالزمن كشعور أو كتقييم مسألة تخضع للكثير من الجدل.
تصف نصوص فيدا (أقدم النصوص التي تتحدث عن الفلسفة الهندية والفلسفة الهندوسية والتي ترجع إلى الألفية الثانية قبل الميلاد[27]) علم الفلك الهندي القديم، وفيها يمر الكون بسلسلة متكررة من الخلق والتدمير والبعث حيث تستغرق كل دورة 4,320 مليون سنة. كتب الفلاسفة اليونانيون القدماء (مثل بارمينيدس وهرقليطس) مقالات عن طبيعة الزمن. عرّف أفلاطون (في طيماوس) الزمن بأنه فترة حركة الأجسام السماوية. عرّف أرسطو (في الكتاب الرابع من السماع الطبيعي) الزمن بأنه عدد من الحركات بالنسبة إلى ما قبل وما بعد.
في الكتاب الحادي عشر من اعترافات القديس أوغسطين، يتأمل أوغسطين في طبيعة الزمن متسائلا: «إذا ما هو الزمن؟ إن لم يسألني أحد، فانا أعرف أنني أتمنى أن أفسر ذلك في حال سألني أحدهم» يشرع أوغسطين بعد ذلك في تعريف الزمن بما لا يعتبر منه بدلا من ما يعتبر منه، وهو أسلوب مشابه للأسلوب الذي اتبعه في التعريفات السالبة.[28] إلا أن القديس أوغسطين انتهى بأن أطلق على الزمن بأنه «تمدد» للعقل والذي من خلاله نستوعب الماضي في ذاكرتنا، والحاضر في انتباهنا، والمستقبل في توقعنا، كل ذلك في نفس الوقت.
تتشارك الأديان الإبراهيمية في هذا المعتقد حيث تعتقد جميعها أن الزمن الكوني بدأ مع الخلق.[بحاجة لتوضيح]
آمن إسحق نيوتن بالمكان المطلق والزمان المطلق، بينما آمن لايبنتس بأن الزمان والمكان نسبيين. برزت الاختلافات بين تفسيرات نيوتن ولايبتس في مراسلات لايبتس كلارك الشهيرة.[29]
وصف إيمانويل كانت –في نقد العقل المحض- الزمن بأنه فكرة بديهية تسمح لنا (مع الفكرة البديهية الأخرى: المكان) باستيعاب الأدلة التجريبية. يعتقد كانت أنه لا المكان ولا الزمان يمكن تصوره كحركة جوهرية، ولكن كلا منهما إطار عقلي نظامي والذي ينشئ أي تجربة عقلية أو ملاحظة تجريبية. رأى كانت الزمن كجزء أساسي من الإطار العقلي للبنية المجردة –مع المكان والعدد- والذي نستخدمه في تسلسل الأحداث، وجعلها كمّية خلال مدتها، ومقارنة حركة الأشياء
أخيرا هذه زبدة البحوث العلمية حول هذا الموضوع نضعها للقاريء والباحث لكي يكون أطلاع واسع على العلوم العصرية والتقنيات الحديثة .
نحن البشر نعيش فى الزمن ولكن ماهو الزمن بالضبط وهل هو يسير إلى الأمام أم إلى الخلف
قبل محاولة الإجابة على هذا التساؤل ينبغي أن نلقي نظرة على شيء إسمه فيزياء الكم حتى نفهم مجريات المادة الزمنية إذا صح لها هذا التعبير
هي نظرية رئيسة في الفيزياء توفر وصفًا للخصائص الفيزيائية للطبيعة على مقياس الذرات والجسيمات دون الذرية.[2] وميكانيكا الكم (أو الحركة الكمومية) هي الأساس الذي تقوم عليه فيزياء الكم وكيمياء الكم ونظرية الحقل الكمومي وتقانة الكم وعلوم المعلومات الكمومية.
تُسمَّى مجموعة النظريات التي كانت موجودةً قبل ظهور ميكانيكا الكم الفيزياء الكلاسيكية، وهي تصف جوانبَ عديدةً من الطبيعة باعتماد مقياس عياني، ولكنها لا تصلح لوصف الظواهر الحاصلة في المقاييس الذرية ودون الذرية. يمكن اشتقاق معظم النظريات في الفيزياء الكلاسيكية من ميكانيكا الكم مثل تقريب صالح على نطاق واسع (عياني).[3]
تختلف ميكانيكا الكم (أو الحركة الكمومية) عن الفيزياء الكلاسيكية في اقتصار الطاقة والزخم والزخم الزاوي (عزم الدوران) والكميات الأخرى من نظام مقيد على القيم المنفصلة (التكميم)، وللأجسام فيها خصائص الجسيمات والموجات معًا (ازدواجية موجة جسيم)؛ وهناك حدود لمدى دقة التنبؤ بقيمة الكمية المادية قبل قياسها، بالنظر إلى مجموعةٍ كاملةٍ من الشروط الأولية (مبدأ اللايقين).
طُوِّرت ميكانيكا الكم تدريجيًا انطلاقًا من نظرياتٍ تشرح الملاحظات التي لا يمكن التوفيق بينها وبين الفيزياء الكلاسيكية، مثل حل ماكس بلانك لمشكلة إشعاع الجسم الأسود في عام 1900، والمطابقة بين الطاقة والتردد في ورقة ألبرت أينشتاين عام 1905 والتي فسرت التأثير الكهروضوئي.[4] أدت هذه المحاولات المبكرة لفهم الظواهر العيانية -والمعروفة الآن باسم «نظرية الكم القديمة»- إلى التطور الكامل لميكانيكا الكم في منتصف عشرينيات القرن الماضي بواسطة نيلز بور وإرفين شرودنغر وفيرنر هايزنبيرغ وماكس بورن وبول ديراك وآخرين. صيغت النظرية الحديثة في أشكال رياضية مختلفة طورت خصيصًا لذلك. يوفر كيان رياضي -هو أحد هذه الأشكال الرياضية، ويسمى دالة الموجة- معلوماتٍ -على شكل سعاتٍ احتماليةٍ- حول قياسات طاقة الجسيم، وزخمه، والخصائص الفيزيائية الأخرى التي قد يتسم بها.
نظرة عامة ومفاهيم رئيسة
تسمح ميكانيكا الكم بحساب خصائص الأنظمة الفيزيائية وسلوكها. وهي تطبق عادةً على الأنظمة المجهرية: كالجزيئات والذرات والجسيمات دون الذرية. وقد أُثبتت قدرتها على الاحتفاظ بالجزيئات المعقدة التي تحتوي على آلاف الذرات،[5] ولكن تطبيقها على البشر يثير مشكلاتٍ فلسفيةٍ، مثل صديق ويغنر، ويظل تطبيقها على الكون كله تخمينيًا.[6] تحقق العلماء من تنبؤات ميكانيكا الكم من خلال التجربة بدرجةٍ عاليةٍ من الدقة.[note 1]
تكمن السمة الرئيسة لميكانيكا الكم في عدم قدرتها على التنبؤ على وجه اليقين بما سيحدث، وتقديمها احتمالاتٍ عوضًا عن ذلك. يُحسَب الاحتمال رياضيًا بأخذ مربع القيمة المطلقة لعدد مركب، والمعروف باسم "سعة الاحتمال". يُعرف هذا باسم قاعدة بورن، والتي سميت على اسم الفيزيائي ماكس بورن. فمثلًا يمكن وصف جسيمٍ كميٍّ مثل الإلكترون بواسطة دالة موجية تربط كل نقطةٍ في الفضاء بسعةٍ احتمالية. إن تطبيق قاعدة بورن على هذه السعات يعطي دالة الكثافة الاحتمالية للموقع الذي سيوجد فيه الإلكترون عند إجراء تجربةٍ لتعيين مكانه، وهذا أفضل ما يمكن للنظرية أن تقدمه؛ فهي لا يمكنها تحديد موقع الإلكترون على وجه اليقين. وتربط معادلة شرودنغر مجموعة السعات الاحتمالية لموقع لإلكترون المتعلقة بلحظةٍ زمنيةٍ معينةٍ بمجموعة السعات الاحتمالية المتعلقة بلحظةٍ زمنيةٍ أخرى.
إحدى نتائج القواعد الرياضية لميكانيكا الكم هي المقايضة حول إمكانية التنبؤ بين الكمومات المختلفة القابلة للقياس. تشير الصيغة الأكثر شهرةَ لمبدأ اللايقين هذا إلى أنه -وبغض النظر عن كيفية تحضير الجسيم الكمي أو مدى دقة ترتيب التجارب عليه- فإن من المستحيل وجود تنبؤٍ دقيقٍ لقياس كلا موقعه وزخمه في الوقت نفسه.
تعد ظاهرة التداخل الكمي إحدى النتائج الأخرى للقواعد الرياضية لميكانيكا الكم، وهي غالبًا ما تتضَّح من خلال تجربة الشق المزدوج. في النسخة الأصلية من هذه التجربة يُضيء مصدر ضوءٍ متسقٍ -كشعاع ليزر مثلًا- صفيحةً مثقوبةً بشقين متوازيين، ويلاحظ الضوء الذي يمر عبر الشقين على شاشةٍ تقع خلف الصفيحة المثقوبة.[2]:1.1–1.8[7]:102–111 تتسبب الطبيعة الموجية للضوء في تداخل موجات الضوء التي تعبر الشقين، مما ينتج عنه نطاقات ساطعة ومظلمة على الشاشة؛ وهي نتيجة لا يمكن توقعها إذا كان الضوء يتكون من جسيماتٍ كلاسيكية.[7] ومع ذلك دائمًا ما يُمتص الضوء على الشاشة عند نقاطٍ منفصلةٍ كجسيماتٍ فرديةٍ بدلًا من موجاتٍ؛ ويَظهر نمط التداخل من خلال الكثافة المتغيرة لاصطدامات هذه الجسيمات على الشاشة. علاوةً على ذلك وَجدت نسخٌ لاحقة للتجربة تتضمن وضع كاشفاتٍ عند الشقوق أن كل فوتون مكتشَفٍ يمر من خلال شقٍّ واحدٍ (كما هو الحال مع الجسيم الكلاسيكي)، وليس عبر كلا الشقين (كما الحال بالنسبة للموجة).[7]:109[8][9] ومع ذلك فإن مثل هذه التجارب تظهر أن الجسيمات لا تشكل نمط التداخل إذا اكتشف المرء الشق الذي تمر من خلاله. عُثر على جسيماتٍ أخرى ذات مقاسٍ ذريٍّ -مثل الإلكترونات- تُظهر السلوك نفسه عند إطلاقها نحو شقٍّ مزدوج.[2] وهو السلوك الذي يُعرف بازدواجية موجة-جسيم.
تنبأت ميكانيكا الكم بظاهرةٍ أخرى غير بدهيّةٍ هي ظاهرة النفق الكمومي، وفيها يمكن للجسيم الذي يتقدم باتجاه حاجز جهدي أن يتخطاه ولو كانت طاقته الحركية أصغر من الحد الأقصى المحتمل.[10] بينما في الميكانيكا الكلاسيكية سيجري احتجاز هذا الجسيم. ثمة نتائج عديدة مهمة للنفق الكمي مرتبطة بالاضمحلال الإشعاعي، وبالاندماج النووي في النجوم، وتطبيقات مثل مجهر المسح النفقي وثنائي المساري النفقي.[11]
عندما تتفاعل الأنظمة الكمومية يمكن أن تكون النتيجة إنشاء تشابك كمي: فتصبح خصائصها متشابكةً لدرجة أن وصف الكل بالاعتماد على الأجزاء الفردية فقط لا يعود ممكنًا. دعا إرفين شرودنغر التشابكَ «... السمةَ المميزةَ لميكانيكا الكم التي تفرض خروجها بالكامل عن خطوط الفكر الكلاسيكية».[12] يتيح التشابك الكمي الخصائص غير البدهيّةِ للتخاطر الزائف الكمي، ويمكن أن يكون موردًا قيّمًا في بروتوكولات الاتصال، مثل توزيع المفاتيح الكمومية والترميز فائق الكثافة.[13] وعلى عكس الاعتقاد الخاطئ الشائع لا يسمح التشابك بإرسال إشاراتِ أسرع من الضوء، كما يتضح من نظرية عدم الاتصال.[13]
ثمة احتمال آخر ممكن ينتج عن التشابك الكمي هو اختبار «المتغيرات الخفية»، وهي خصائص افتراضية أكثر جوهريةً من الكمومات التي تتناولها نظرية الكم نفسها، ومن شأنها أن تسمح بتنبؤاتٍ أكثر دقةً مما توفره نظرية الكم. أظهرت مجموعة من النتائج -وأهمها مبرهنة بل- أن الفئات العريضة من نظريات المتغيرات الخفية هي في الواقع غير متوافقةٍ مع فيزياء الكم. وفقًا لمبرهنة بل إذا كانت الطبيعة تعمل بالفعل طبقًا لأي نظريةٍ لمتغيراتٍ محليةٍ خفيةٍ، فإن نتائج "اختبار بل" ستكون مقيَّدةً بطريقةٍ معينةٍ قابلةٍ للقياس الكمي. أجري العديد من اختبارات بل باستخدام جسيماتٍ متشابكةٍ، وقد أظهرت نتائجَ غير متوافقةٍ مع القيود التي تفرضها المتغيرات الخفية المحلية.[14][15]
من غير الممكن تقديم هذه المفاهيم بأكثرَ من طريقةٍ سطحيةٍ دون تقديم الرياضيات الفعلية المعنية؛ لا يتطلب فهم ميكانيكا الكم معالجة الأعداد المركبة فحسب، بل أيضًا الجبر الخطي والمعادلات التفاضلية ونظرية الزمر وموضوعاتٍ أخرى أكثر تقدمًا.[note 2] وفقًا لذلك ستقدم هذه المقالة صياغةً رياضيةً لميكانيكا الكم ومسحًا لتطبيقاتها على بعض الأمثلة المفيدة التي جرت دراستها كثيرًا.
صياغة رياضية
المقالة الرئيسة: صياغة رياضية لميكانيكا الكم
تكون حالة النظام الميكانيكي الكمومي في الصيغة الرياضية الدقيقة لميكانيكا الكم عبارةً عن متجه � ينتمي إلى فضاء هيلبرت العقدي (القابل للفصل) �
ينتمي إلى فضاء هيلبرت العقدي (القابل للفصل) � . يُفترض أن هذا المتجه يجري تطبيعه ضمن الجداء الداخلي لفضاء هيلبرت، أي إنه يخضع لـ⟨�,�⟩=1
. يُفترض أن هذا المتجه يجري تطبيعه ضمن الجداء الداخلي لفضاء هيلبرت، أي إنه يخضع لـ⟨�,�⟩=1 ، وهو محدد جيد حتى عدد معقد من المعامل 1 (المرحلة العامة)، أي �
، وهو محدد جيد حتى عدد معقد من المعامل 1 (المرحلة العامة)، أي � style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1028"> و����
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1028"> و���� style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle e^{i\alpha }\psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1029"> تمثل النظام الفعلي نفسه. بعبارةٍ أخرى الحالات المحتملة هي نقاط في الفضاء الإسقاطي لفضاء هيلبرت، والتي تسمى عادةً فضاء الإسقاط العقدي. تعتمد الطبيعة الدقيقة لفضاء هيلبرت على النظام؛ فعلى سبيل المثال لوصف الموقع والزخم، فإن فضاء هيلبرت هو فضاء الدوال العقدية القابلة للتكامل المربع �2(�)
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle e^{i\alpha }\psi }" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1029"> تمثل النظام الفعلي نفسه. بعبارةٍ أخرى الحالات المحتملة هي نقاط في الفضاء الإسقاطي لفضاء هيلبرت، والتي تسمى عادةً فضاء الإسقاط العقدي. تعتمد الطبيعة الدقيقة لفضاء هيلبرت على النظام؛ فعلى سبيل المثال لوصف الموقع والزخم، فإن فضاء هيلبرت هو فضاء الدوال العقدية القابلة للتكامل المربع �2(�) style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle L^{2}(\mathbb {C} )}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1030">، بينما فضاء هلبرت لمغزل بروتون واحد هو ببساطة فضاء المتجهات العقدية ثنائية الأبعاد �2
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle L^{2}(\mathbb {C} )}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1030">، بينما فضاء هلبرت لمغزل بروتون واحد هو ببساطة فضاء المتجهات العقدية ثنائية الأبعاد �2 style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \mathbb {C} ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1031"> مع الجداء الداخلي المعتاد.
style='max-height: 1e+06px;box-sizing: inherit' alt="{\displaystyle \mathbb {C} ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1031"> مع الجداء الداخلي المعتاد.
يجري تمثيل الكمومات المادية ذات الأهمية -الموقع، والزخم، والطاقة، والمغزلية- بواسطة المراقبات، وهي مؤثرات خطية هيرميتية (بتعبيرٍ أدق مساعد ذاتي) تعمل في فضاء هيلبرت. يمكن أن تكون الحالة الكمومية متجهًا ذاتيًا يمكن ملاحظته، وفي هذه الحالة يطلق عليها اسم حالة ذاتية، وتتوافق القيمة الذاتية المرتبطة مع قيمة ما يمكن ملاحظته في تلك الحالة الذاتية. ستكون الحالة الكمومية مزيجًا خطيًا من حالاتٍ ذاتيةٍ عموماً، والمعروف باسم التراكب الكمومي. عندما يجري قياس ما يمكن ملاحظته، ستكون النتيجة واحدة من قيمها الذاتية مع الاحتمال الذي قدمته قاعدة بورن: في أبسط الحالات، تكون القيمة الذاتية � غير منهارةٍ ويجري إعطاء الاحتمال بواسطة |⟨�→,�⟩|2
غير منهارةٍ ويجري إعطاء الاحتمال بواسطة |⟨�→,�⟩|2 ، وفيه �→
، وفيه �→ هو المتجه الذاتي المرتبط به. تنهار القيمة الذاتية عادةً ويُعطى الاحتمال باستعمال ⟨�,���⟩
هو المتجه الذاتي المرتبط به. تنهار القيمة الذاتية عادةً ويُعطى الاحتمال باستعمال ⟨�,���⟩ ، وفيه ��
، وفيه �� هو الإسقاط على الفضاء الذاتي المرتبطة به. في الحالة المستمرة تعطي هذه الصيغ بدلاً من ذلك كثافة الاحتمال.
هو الإسقاط على الفضاء الذاتي المرتبطة به. في الحالة المستمرة تعطي هذه الصيغ بدلاً من ذلك كثافة الاحتمال.
إذا تُوُصِّلَ -بعد القياس- إلى النتيجة � فيُفترض أن الحالة الكمومية تنهار إلى �→
فيُفترض أن الحالة الكمومية تنهار إلى �→ ، في الحالة غير المنهارة أو ���/⟨�,���⟩
، في الحالة غير المنهارة أو ���/⟨�,���⟩ في الحالة العامة. وعليه فإن الطبيعة الاحتمالية لميكانيكا الكم تنبع من فعل القياس، وهو أحد أصعب جوانب الأنظمة الكمومية قابليةً للفهم، وقد كان الموضوع الرئيسي في مناظرات بور-أينيشتاين الشهيرة، حيث حاول فيها العالمان توضيح هذه المبادئ الرئيسة عن طريق التجارب الفكرية. وفي العقود التي تلت صياغة ميكانيكا الكم جرت دراسة مسألة ماهية «القياس» على نطاقٍ واسع، وصيغت تفسيرات جديدة لميكانيكا الكم تتخلص من مفهوم «انهيار الدالة الموجية» (انظر على سبيل المثال تفسير العوالم المتعددة). الفكرة الأساس هي أن دوال الموجة الخاصة بنظامٍ كميٍّ وجهاز قياسٍ تتشابك عندما يتفاعلان، وحينها يتوقف النظام الكمي الأصيل عن الوجود بصفته كيانًا مستقلًا. لمزيدٍ من التفاصيل راجع مقال القياس في ميكانيكا الكم.[18]
في الحالة العامة. وعليه فإن الطبيعة الاحتمالية لميكانيكا الكم تنبع من فعل القياس، وهو أحد أصعب جوانب الأنظمة الكمومية قابليةً للفهم، وقد كان الموضوع الرئيسي في مناظرات بور-أينيشتاين الشهيرة، حيث حاول فيها العالمان توضيح هذه المبادئ الرئيسة عن طريق التجارب الفكرية. وفي العقود التي تلت صياغة ميكانيكا الكم جرت دراسة مسألة ماهية «القياس» على نطاقٍ واسع، وصيغت تفسيرات جديدة لميكانيكا الكم تتخلص من مفهوم «انهيار الدالة الموجية» (انظر على سبيل المثال تفسير العوالم المتعددة). الفكرة الأساس هي أن دوال الموجة الخاصة بنظامٍ كميٍّ وجهاز قياسٍ تتشابك عندما يتفاعلان، وحينها يتوقف النظام الكمي الأصيل عن الوجود بصفته كيانًا مستقلًا. لمزيدٍ من التفاصيل راجع مقال القياس في ميكانيكا الكم.[18]
جرى وصف النمو الزمني للحالة الكمومية بواسطة معادلة شرودنغر:
�ℏ����(�)=��(�)
وتشير � فيها إلى هاملتوني يمكن ملاحظته المقابلة للطاقة الكلية للنظام، وℏ
فيها إلى هاملتوني يمكن ملاحظته المقابلة للطاقة الكلية للنظام، وℏ هو ثابت بلانك المختزَل. يُدخل الثابت �ℏ
هو ثابت بلانك المختزَل. يُدخل الثابت �ℏ لكي يقلل هاميلتوني إلى هاملتونيان الكلاسيكي في الحالات التي يُقرَّب فيها النظام الكمومي باستعمال النظام الكلاسيكي؛ وتسمى القدرة على إجراء مثل هذا التقريب في حدودٍ معينةٍ مبدأ التطابق.
لكي يقلل هاميلتوني إلى هاملتونيان الكلاسيكي في الحالات التي يُقرَّب فيها النظام الكمومي باستعمال النظام الكلاسيكي؛ وتسمى القدرة على إجراء مثل هذا التقريب في حدودٍ معينةٍ مبدأ التطابق.
يُعطى حل هذه المعادلة التفاضلية كما يأتي:
�(�)=�−���/ℏ�(0)
يُعرف عامل المؤثر �(�)=�−���/ℏ باسم عامل النمو الزمني ولديه الخاصة الحاسمة بأنه وحدوي. يعتبر النمو الزمني هذا حتميًا بمعنى أنه -بالنظر إلى حالةٍ كموميةٍ أوليةٍ �(0)
باسم عامل النمو الزمني ولديه الخاصة الحاسمة بأنه وحدوي. يعتبر النمو الزمني هذا حتميًا بمعنى أنه -بالنظر إلى حالةٍ كموميةٍ أوليةٍ �(0) - يقدم تنبؤًا محددًا لماهية الحالة الكمية �(�)
- يقدم تنبؤًا محددًا لماهية الحالة الكمية �(�) في أي وقت لاحق.[19]
في أي وقت لاحق.[19]
كثافات الاحتمالية المقابلة للدوال الموجية للإلكترون في ذرة الهيدروجين التي تمتلك مستويات طاقة محددة (تزداد من أعلى الصورة إلى الأسفل: ... ,n = 1, 2, 3) والعزم الزاوي (يزداد من اليسار إلى اليمين: ... ,s, p, d). تتوافق المناطق الأكثر كثافة مع كثافة احتمالية أعلى في قياس الموقع. يمكن مقارنة دوال الموجة هذه مباشرة بأرقام كلادني للأنماط الصوتية للاهتزاز في الفيزياء الكلاسيكية وهي أنماط من التذبذب أيضًا، تمتلك طاقة محددة وبالتالي ترددًا محددًا. يجري قياس الزخم الزاوي والطاقة ويأخذان قيمًا منفصلة فقط مثل تلك الموضحة (كما الحال بالنسبة للترددات الرنانة في الصوتيات).
من خلال دوال الموجة «المتزنة». على سبيل المثال يُصوَّر إلكترون واحد في ذرة غير مستثارةٍ تصويراً تقليدياً على هيئة جسيمٍ متحرِّكٍ في مسارٍ دائريٍّ حول النواة الذرية، بينما يجري وصفه في ميكانيكا الكم بواسطة دالة موجةٍ متزنةٍ تحيط بالنواة. مثلًا دالة الموجة الإلكترونية لذرة هيدروجينٍ غير مستثارةٍ هي دالة متناظرة كرويًا تُعرف باسم مدار s (الشكل 1).
تُعرف الحلول التحليلية لمعادلة شرودنغر بعددٍ قليلٍ جدًا من النماذج البسيطة نسبيًا من أتباع هاميلتونيين بما في ذلك الهزاز التوافقي الكمومي والجسيم في الصندوق وكاتيون ثنائي الهيدروجين وذرة الهيدروجين. حتى ذرة الهليوم -التي تحتوي على إلكترونين فقط- تحدت جميع المحاولات في علاجٍ تحليليٍّ كامل.
ومع هذا ثمة تقانات لإيجاد حلولٍ تقريبية. تستخدم إحدى الطرق -المسماة نظرية الاضطراب- النتيجة التحليلية لنموذجٍ ميكانيكيٍّ كميٍّ بسيطٍ لإنشاء نتيجةٍ لنموذجٍ ذي صلةٍ، ولكنه أكثر تعقيدًا -على سبيل المثال- عن طريق إضافة طاقةٍ كامنةٍ ضعيفة. هناك طريقة أخرى تسمى «معادلة الحركة شبه الكلاسيكية»، والتي تنطبق على الأنظمة التي ينتج عنها ميكانيكا الكم انحرافات صغيرة فقط عن السلوك الكلاسيكي. يمكن بعد ذلك حساب هذه الانحرافات بناءً على الحركة الكلاسيكية. هذا النهج مهم خصوصاً في حقل الفوضى الكمومية.
مبدأ اللايقين
إحدى النتائج الرئيسة للصيغ الكمومية هي مبدأ اللايقين. ينص هذا المبدأ في أكثر أشكاله شيوعًا على أنه لا يوجد تحضير لجسيمٍ كميٍّ يمكن أن يشير ضمنًا إلى تنبؤاتٍ دقيقةٍ في الوقت نفسه لتحديد موقعه وقياس زخمه.[20][21] كل من الموقع والزخم يمكن ملاحظتهما، مما يعني أنهما ممثَّلان من قبل المؤثرات الهيريميتية. مؤثر الموقع �^ ومؤثر الزخم �^
ومؤثر الزخم �^ لا يستبدان بل يلبيان علاقة التبديل القانوني:
لا يستبدان بل يلبيان علاقة التبديل القانوني:
[�^,�^]=�ℏ![{\displaystyle [{\hat {X}},{\hat {P}}]=i\hbar }](http:///C:\Users\qcer\AppData\Local\Temp\msohtmlclip1\01\clip_image001.gif)
وبالنظر إلى الحالة الكمومية تتيح لنا قاعدة بورن حساب قيم التوقع لكل من � و�
و� ، بالإضافة إلى قوى كل منهما. تحديد اللايقين للملاحظة من خلال الانحراف المعياري، لدينا
، بالإضافة إلى قوى كل منهما. تحديد اللايقين للملاحظة من خلال الانحراف المعياري، لدينا
��=⟨�2⟩−⟨�⟩2
وبالمثل بالنسبة للزخم:
��=⟨�2⟩−⟨�⟩2 alt="{\displaystyle \sigma _{P}={\sqrt {\langle {P}^{2}\rangle -\langle {P}\rangle ^{2}}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1054">
alt="{\displaystyle \sigma _{P}={\sqrt {\langle {P}^{2}\rangle -\langle {P}\rangle ^{2}}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1054">
ينص مبدأ اللايقين على ذلك
����≥ℏ2 ' alt="{\displaystyle \sigma _{X}\sigma _{P}\geq {\frac {\hbar }{2}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1055">
' alt="{\displaystyle \sigma _{X}\sigma _{P}\geq {\frac {\hbar }{2}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1055">
يمكن نظرياً أن يكون أي من الانحرافين المعياريين ذا قيمةٍ صغيرةٍ عشوائيًّا، ولكن ليس كلاهما في وقتٍ واحد.[22] تُعمَّم هذه المتباينة على أزواجٍ عشوائيةٍ من المؤثرات المترابطة ذاتيًا � alt="{\displaystyle A}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1056"> و�
alt="{\displaystyle A}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1056"> و� . المبدل لهذين الموثرين هو
. المبدل لهذين الموثرين هو
[�,�]=��−�� ' alt="{\displaystyle [A,B]=AB-BA}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1058">
' alt="{\displaystyle [A,B]=AB-BA}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1058">
وهذا يوفر الحد الأدنى لجداء الانحرافات المعيارية:
����≥12|⟨[�,�]⟩|![{\displaystyle \sigma _{A}\sigma _{B}\geq {\frac {1}{2}}\left|\langle [A,B]\rangle \right|}](http:///C:\Users\qcer\AppData\Local\Temp\msohtmlclip1\01\clip_image001.gif)
ثمة نتيجة أخرى لعلاقة التبديل القانوني وهي أن مؤثري الموقع والزخم عبارة عن تحويلات فورييه لبعضهم بعضَا، فيكون وصف كائنٍ وفقًا لزخمه الخاص به هو تحويل فورييه لوصفه وفقًا لموقعه. وحقيقةً إن الاعتماد في الزخم هو تحويل فورييه للاعتماد في الموقع يعني أن مؤثر الزخم مكافئ (حتى عامل �/ℏ ) لأخذ المشتق وفقًا للموقع، لأن التمايز في تحليل فورييه يتوافق مع الضرب في الفضاء المزدوج، وهو السبب في المعادلات الكمومية في فضاء الموقع، يستبدل الزخم ��
) لأخذ المشتق وفقًا للموقع، لأن التمايز في تحليل فورييه يتوافق مع الضرب في الفضاء المزدوج، وهو السبب في المعادلات الكمومية في فضاء الموقع، يستبدل الزخم �� بـ−�ℏ∂∂�
بـ−�ℏ∂∂� alt="{\displaystyle -i\hbar {\frac {\partial }{\partial x}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1062">، وعلى وجه الخصوص في معادلة شرودنغر غير النسبية في فضاء الموقع، يستبدل مصطلح مربع الزخم بضرب لابلاسيه −ℏ2
alt="{\displaystyle -i\hbar {\frac {\partial }{\partial x}}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1062">، وعلى وجه الخصوص في معادلة شرودنغر غير النسبية في فضاء الموقع، يستبدل مصطلح مربع الزخم بضرب لابلاسيه −ℏ2 ' alt="{\displaystyle -\hbar ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1063"> .[20]
' alt="{\displaystyle -\hbar ^{2}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1063"> .[20]
الأنظمة المركبة والتشابك
عندما ينظر إلى نظامين كموميين مختلفين معًا، فإن فضاء هيلبرت للنظام المدمج هو ناتج جداء الموتر لفضاءات هيلبرت للمكونين. مثلًا لنفترض أن A وB نظامان كموميان مع فضاءات هيلبرت �� alt="{\displaystyle {\mathcal {H}}_{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1064"> و��
alt="{\displaystyle {\mathcal {H}}_{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1064"> و�� alt="{\displaystyle {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1065"> على التوالي. إذن فضاء هيلبرت للنظام المركب هو
alt="{\displaystyle {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1065"> على التوالي. إذن فضاء هيلبرت للنظام المركب هو
���=��⊗�� alt="{\displaystyle {\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1066">
alt="{\displaystyle {\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1066">
إذا كانت حالة النظام الأول هي المتجه �� alt="{\displaystyle \psi _{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1067"> وكانت حالة النظام الثاني هي ��
alt="{\displaystyle \psi _{A}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1067"> وكانت حالة النظام الثاني هي �� alt="{\displaystyle \psi _{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1068">، فإن حالة النظام المركب هي
alt="{\displaystyle \psi _{B}}" class="mwe-math-fallback-image-inline mw-invert skin-invert" aria-hidden=true v:shapes="_x0000_i1068">، فإن حالة النظام المركب هي
��⊗��
لا يمكن كتابة جميع الحالات في فضاء هيلبرت المشترك ��� بهذا الشكل، لأن مبدأ التراكب يشير إلى أن التوليفات الخطية لهذه الحالات «القابلة للفصل» أو «حالات المنتج» صالحة أيضًا. على سبيل المثال إذا كانت كلتا ��
بهذا الشكل، لأن مبدأ التراكب يشير إلى أن التوليفات الخطية لهذه الحالات «القابلة للفصل» أو «حالات المنتج» صالحة أيضًا. على سبيل المثال إذا كانت كلتا �� و��
و�� حالتان ممكنتان للنظام �
حالتان ممكنتان للنظام � وبالمثل ��
وبالمثل �� و��
و�� كلتاهما حالتان ممكنتان للنظام �
كلتاهما حالتان ممكنتان للنظام � إذن
إذن
12(��⊗��+��⊗��)
هي حالة مشتركة صالحة لا يمكن فصلها، والحالات غير القابلة للفصل تسمى متشابكة.[23][24]
إذا كانت حالة النظام المركب متشابكةً فمن المستحيل وصف أي نظام مكون A أو النظام B بواسطة متجه الحالة. يمكن للمرء بدلاً من ذلك تحديد مصفوفات الكثافة المنخفضة التي تصف الإحصائيات التي يمكن الحصول عليها من خلال إجراء قياساتٍ على أي نظامٍ مكونٍ بمفرده. يؤدي هذا بالضرورة إلى فقدان المعلومات، على الرغم من أن معرفة مصفوفات الكثافة المنخفضة للأنظمة الفردية لا يكفي لإعادة بناء حالة النظام المركب.[23][24] تمامًا كما تحدد مصفوفات الكثافة حالة نظامٍ فرعيٍّ لنظامٍ أكبر. بالمقابل تصف (POVMs) التأثير على نظام فرعي للقياس الذي يجري على نظام أكبر. تستخدم POVM على نطاق واسع في نظرية المعلومات الكمومية.[23][25]
وكما هو موضح أعلاه يعد التشابك سمة رئيسة لنماذج عمليات القياس التي تتشابك فيها الأدوات مع النظام الذي يجري قياسه. تتفاعل الأنظمة متشابكة مع البيئة حيث توجد، وهي ظاهرة تُعرف باسم إزالة الترابط الكمي. هذا يمكن أن يفسر لماذا -من الناحية العملية- تصعب ملاحظة التأثيرات الكمية في الأنظمة الأكبر من المجهرية.[26]
التكافؤ بين الصيغ
توجد صيغ عديدة متكافئة رياضيًا لوصف ميكانيكا الكم، أقدمها وأشهرها هي «نظرية التحويل» التي اقترحها بول ديراك، والتي توحد وتعمم الصيغتين الأقدم لميكانيكا الكم؛ ميكانيكا المصفوفة (وضعها فيرنر هايزنبيرغ) وميكانيكا الموجات (وضعها إرفين شرودنغر).[27] الصيغة البديلة لميكانيكا الكم هي صيغة فاينمان لتكامل المسار، وفيها يُنظر إلى السعة الميكانيكية الكمومية بوصفها مجموعاً للمسارات التقليدية وغير التقليدية الممكنة بين الوضعين الابتدائي والنهائي. هذا هو المقابل الميكانيكي الكمومي لمبدأ الفعل في الميكانيكا التقليدية.
التناظرات وقوانين الحفظ
المقالة الرئيسة: مبرهنة نويثر
يُعرف هاميلتونيان � بأنه مُولِّد نمو الوقت، لأنه يحدد عامل النمو الزمني الوحدوي �(�)=�−���/ℏ
بأنه مُولِّد نمو الوقت، لأنه يحدد عامل النمو الزمني الوحدوي �(�)=�−���/ℏ لكل قيمة من قيم �
لكل قيمة من قيم � . يترتب على هذه العلاقة بين �(�)
. يترتب على هذه العلاقة بين �(�) و�
و� حفظ �
حفظ � ويمكن ملاحظته أن توقُّع �
ويمكن ملاحظته أن توقُّع � : لن يُغير القيمة بمرور الوقت. تُعمم هذه العبارة رياضيًا أي عامل هرميتي �
: لن يُغير القيمة بمرور الوقت. تُعمم هذه العبارة رياضيًا أي عامل هرميتي � يمكن أن يولد مجموعةً من العوامل الوحدوية ذات معلماتٍ بواسطة متغير �
يمكن أن يولد مجموعةً من العوامل الوحدوية ذات معلماتٍ بواسطة متغير � . في ظل التطور الناتج عن �
. في ظل التطور الناتج عن � ، سيجري حفظ أي �
، سيجري حفظ أي � يمكن ملاحظته ويتنقل مع �
يمكن ملاحظته ويتنقل مع � . علاوةً على ذلك إذا كان �
. علاوةً على ذلك إذا كان � محفوظًا بالنمو تحت �
محفوظًا بالنمو تحت � ، فإن �
، فإن � يجري حفظه في ظل النمو الناتج عن �
يجري حفظه في ظل النمو الناتج عن � . يشير هذا إلى نسخةٍ كميةٍ للنتيجة التي أثبتتها إيمي نويثر في الميكانيكا الكلاسيكية (لاغرانج): لكل تناظرٍ قابلٍ للاشتقاق الهاملتوني يوجد قانون حفظ مطابق
. يشير هذا إلى نسخةٍ كميةٍ للنتيجة التي أثبتتها إيمي نويثر في الميكانيكا الكلاسيكية (لاغرانج): لكل تناظرٍ قابلٍ للاشتقاق الهاملتوني يوجد قانون حفظ مطابق
تقول النظرية الجديدة إنه قد يكون هناك "كون آخر مضاد"، يعود إلى الوراء في الزمن قبل الانفجار العظيم.
وتفترض النظرية أن الكون المبكر كان صغيرًا وساخنًا وكثيفًا ومنتظمًا لدرجة أن الوقت يبدو متماثلًا بالتقدم للأمام وللخلف. وإذا كان هذا صحيحًا ، فإن النظرية الجديدة تعني أن المادة المظلمة ليست غامضة جدًا، وإنها مجرد ظل جديدة لجسيم شبحي يسمى "نيوترينو" لا يمكن أن يوجد إلا في هذا النوع من الكون
وتشير النظرية إلى أنه لن تكون هناك حاجة لفترة "تضخم" توسعت بسرعة في حجم الكون الشاب بعد فترة وجيزة من الانفجار العظيم. إذا كان هذا صحيحًا، فإن التجارب المستقبلية للبحث عن موجات الجاذبية، أو لتحديد كتلة النيوترينوات، يمكن أن تجيب بشكل نهائي عما إذا كان هذا الكون المرآة المضاد موجودًا.
حدد الفيزيائيون مجموعة من التناظرات الأساسية في الطبيعة. أهم ثلاثة تناظرات هي: الشحنة (إذا قلبت شحنات جميع الجسيمات المشاركة في تفاعل مع الشحنة المعاكسة ، فستحصل على نفس التفاعل)، التكافؤ (إذا نظرت إلى الصورة المتطابقة للتفاعل ، تحصل على نفس النتيجة)، والوقت (إذا قمت بتشغيل تفاعل إلى الوراء في الوقت المناسب ، فسيبدو هو نفسه).
تخضع التفاعلات الفيزيائية لمعظم هذه التناظرات في معظم الأوقات، مما يعني أنه توجد أحيانًا انتهاكات. لكن الفيزيائيين لم يلاحظوا أبدًا انتهاكًا لمجموعة من التماثلات الثلاثة في نفس الوقت. إذا أخذت كل تفاعل لوحظ في الطبيعة وقلبت الشحنات ، وأخذت صورة معكوسة ، وقمت بتشغيلها للخلف في الوقت المناسب ، فإن هذه التفاعلات تتصرف تمامًا.
يتم إعطاء هذا التناظر الأساسي اسمًا: تناظر CPT ، للشحنة (C) ، التكافؤ (P) والوقت (T).
وفي دراسة بحثية جديدة تم قبولها مؤخرًا للنشر في مجلة حوليات الفيزياء، اقترح العلماء توسيع هذا التناظر المشترك. عادةً ما ينطبق هذا التناظر فقط على التفاعلات - القوى والمجالات التي تشكل فيزياء الكون. لكن ربما، إذا كان هذا التناظر مهما للغاية، فإنه ينطبق على الكون بأكمله نفسه.
بعبارة أخرى، تمتد هذه الفكرة من هذا التناظر من مجرد تطبيق على "الجهات الفاعلة" في الكون (القوى والحقول) إلى "المرحلة" نفسها ، الشيء المادي الكامل للكون. خلق المادة المظلمة نحن نعيش في عالم يتسع.
هذا الكون مليء بالعديد من الجسيمات التي تقوم بالكثير من الأشياء المثيرة للاهتمام ، وتطور الكون يتحرك إلى الأمام بمرور الوقت. إذا قمنا بتوسيع مفهوم تناظر CPT ليشمل الكون بأكمله ، فإن نظرتنا للكون لا يمكن أن تكون الصورة الكاملة. بدلا من ذلك ، يجب أن يكون هناك المزيد. للحفاظ على تناظر CPT في جميع أنحاء الكون ، يجب أن يكون هناك كوزموس صورة معكوسة يوازن بيننا. سيكون لهذا الكون جميع الشحنات المعاكسة أكثر مما لدينا ، وينقلب في المرآة ، ويعود إلى الوراء في الوقت المناسب. كوننا مجرد توأم. مجتمعة ، يطيع الكونان تناظر CPT.
ووجد الباحثون أن الشروط المفروضة من خلال الانصياع لتناظر CPT سوف تملأ كوننا بالنيوترينوات اليمنى، وهو ما يكفي لتفسير المادة المظلمة.
تنبؤات في المرآة
لن نتمكن من الوصول إلى توأمنا، لأنه موجود "خلف" الانفجار العظيم ، قبل بداية كوننا. لكن هذا لا يعني أنه لا يمكننا اختبار هذه الفكرة.
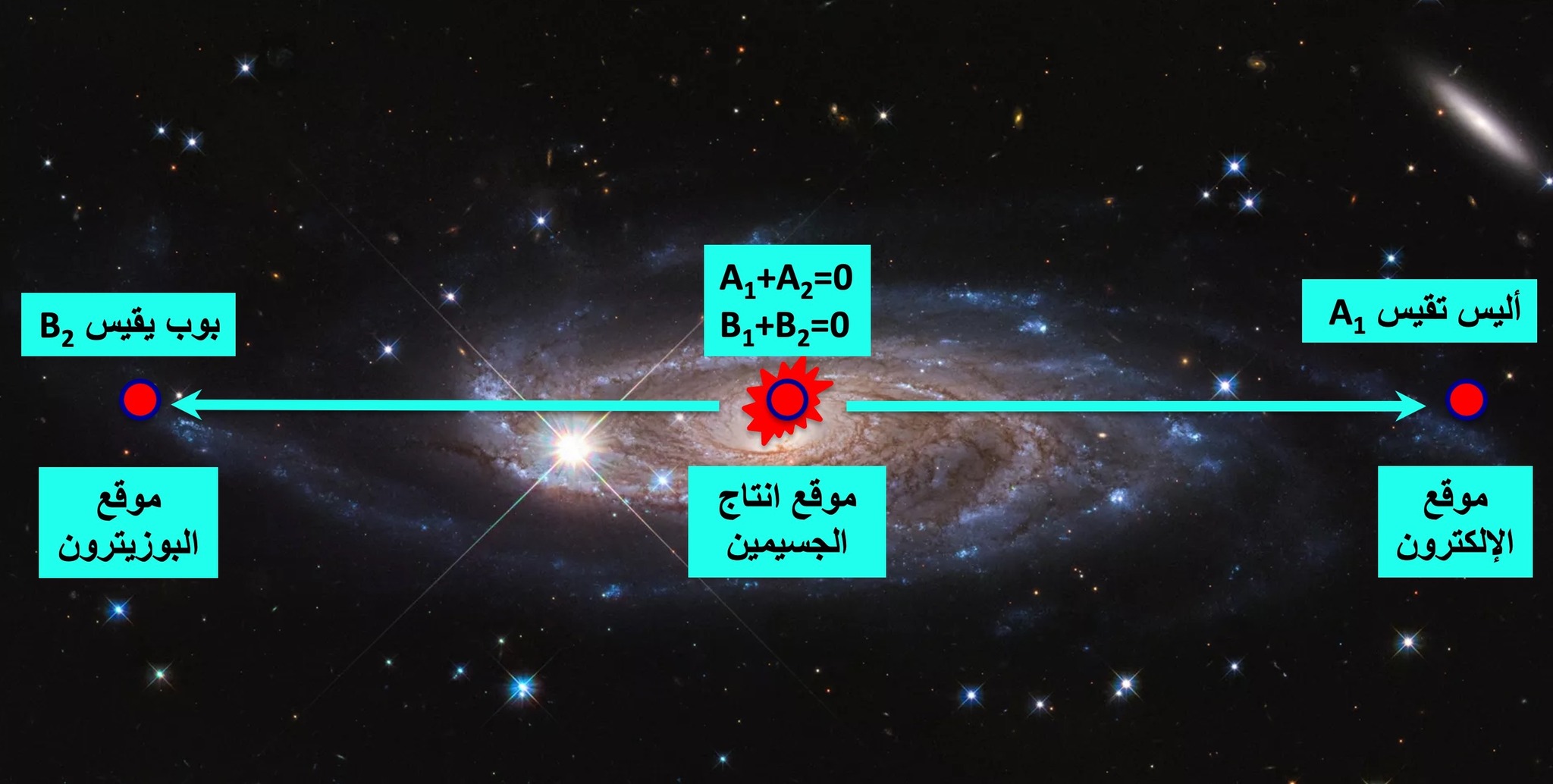
وجد الباحثون بعض النتائج الملاحظة لهذه الفكرة. على سبيل المثال ، توقعوا أن أنواع النيوترينو الثلاثة المعروفة يجب أن تكون جميعها جسيمات ماجورانا، مما يعني أن جزيئاتها المضادة (على عكس الجسيمات العادية مثل الإلكترون، التي لها نظائر من المادة المضادة تسمى البوزيترونات). حتى الآن، علماء الفيزياء ليسوا متأكدين مما إذا كانت النيوترينوات تمتلك هذه الخاصية أم لا.
بالإضافة إلى ذلك ، توقعوا أن يكون أحد أنواع النيوترينو عديم الكتلة. في الوقت الحالي ، يمكن للفيزيائيين فقط وضع حدود عليا لكتل النيوترينو. إذا تمكن الفيزيائيون من قياس كتل النيوترينو بشكل قاطع ، وكان أحدهم عديم الكتلة بالفعل ، فإن ذلك سيعزز بشكل كبير فكرة الكون المتماثل CPT.
أما الزمن فتعريفه قد يكون صعبا ولكن يقال أنالزمن هو عملية تقدم الأحداث بشكلٍ مستمر وإلى أجل غير مسمى بدءًا من الماضي مروراً بالحاضر وحتى المستقبل، وهي عملية لا رجعة فيها/متعذر إلغاؤها.[1][2][3] ربما يكون مصطلح الزمن الأعصى على التعريف، فالزمن أمر نحس به أو نقيسه أو نقوم بتخمينه، وهو يختلف باختلاف وجهة النظر التي ننظر بها بحيث يمكننا الحديث عن زمن نفسي أو زمن فيزيائي أو زمن تخيلي.
لكن يمكننا حصر الزمن مبدئيًا بالإحساس الجماعي للناس كافة على توالي الأحداث بشكل لا رجوع فيه، هذا التوالي الذي يتجلى أكثر ما يتجلى بتوالي الليل والنهار وتعاقب الأيام فرض على الناس تخيل الزمن بشكل نهر جار باتجاه محدد لا عودة فيه.
مع الأيام لاحظ البشر أن العديد من الظواهر الفيزيائية بدءًا من حركات الشمس إلى تساقط الرمل من وعاء زجاجي إلى اهتزاز نوّاس بسيط تأخذ فترات زمنية متساوية حسب تقديرهم مما دفعهم لتطوير ميقاتيات وأدوات لقياس الزمن باستخدام هذه الظواهر فأوجدوا المزولة الشمسية ثم الساعة الرملية ثم ساعة النواس أو البندول.
وفي كل هذه الأزمان تم اعتبار الزمن على أنه أحد المطلقات فالفترات الزمنية الفاصلة بين حدثين مختلفين ثابت بالنسبة لكافة المراقبين، وهذا أمر حافظ عليه نيوتن باعتباره الزمن شيئا مطلقا كونيا فتغيرات الزمن ثابتة في جميع أنحاء الكون، وهو يجري أبدًا كما هو بالنسبة لجملة فيزيائية تتحرك بانتظام أو بتسارع، تتحرك حركة دائرية أو مستقيمة.
ما زال هذا المفهوم للزمن منتشرًا بين الناس كونه يطابق كثيرًا إحساسهم به إلا أن الفيزياء الحديثة قامت بإنزال الزمن عن عرشه وإلغاء صفة الإطلاق التي اتصف بها عبر السنين، فنظرية النسبية الخاصة اعتبرته أحد مكونات المسرح الكوني التي تجري فيه الأحداث وبالتالي أصبحت لكل جملة فيزيائية زمنها الخاص بها الذي يختلف عن زمن جملة فيزيائية أخرى.
قياس الزمن والتاريخ
بصورة عامة، أخذت طرق قياس الزمن صورتين منفصلتين: التقويم وهو أداة رياضية لتنظيم الفترات الزمنية، والساعة وهي آلة ميكانيكية تقيس مرور الوقت.[4] في الحياة اليومية، يتم الرجوع إلى الساعة في الفترات أقل من يوم بينما يتم الرجوع إلى التقويم في الفترات الأطول من يوم. بصورة متزايدة، تُظهر الأجهزة الكهربائية الشخصية كلا من التقويم والساعة في نفس الوقت.
تاريخ التقويم
تقترح الآثار من العصر الحجري القديم أن القمر كان يُستخدم في تقدير الوقت لأكثر من 6000 سنة. كان التقويم القمري من أول التقويمات ظهوراً حيث يتكون من 12 أو 13 شهرا قمريا (354 أو 384 يوما).[5] بدون ضبط التاريخ بطريقة الإقحام لإضافة أيام أو شهور لبعض السنوات، تنحرف الفصول سريعاً في تقويم مبني فقط على اثني عشر شهراً قمرياً. في التقويم الشمسي القمري شهرا إضافيا يُضاف لبعض السنوات للتعويض عن الفرق بين السنة الكاملة (المعروفة الآن بأنها حوالي 365.24 يوما) وبين سنة من اثني عشر شهرا قمريا. ظهرت الأرقام اثنا عشر وثلاثة عشر للتمييز في الكثير من الثقافات، جزئيا على الأقل بسبب هذه العلاقة بين الشهور والسنوات. ظهرت صور مبكرة أخرى للتقويم في أمريكا الوسطى، وخاصة في حضارة المايا القديمة. كان هذا التقويم دينيا فلكيا به 18 شهر في السنة و20 يوما في الشهر بالإضافة إلى خمسة أيام إضافية في نهاية كل عام.[6]
وضعت إصلاحات يوليوس قيصر في 45 ق.م الإمبراطورية الرومانية على تقويم شمسي. كان هذا التقويم اليولياني خاطئا حيث أن إقحامه كان لا يزال يسمح للانقلاب الشمسي والاعتدال الشمسي بالتقدم عكسه بحوالي 11 دقيقة في السنة. قدم البابا غريغوريوس الثالث عشر تصحيحا في 1582، وبدأت دول متعددة اعتماد التقويم الميلادي على مدار عدة قرون، ولكنه الآن أكثر تقويم مستخدم حول العالم بفارق كبير.
أثناء الثورة الفرنسية، تم اقتراح ساعة وتقويم جدد في محاولة لإعادة الوقت إلى المسيحية وخلق نظام أكثر عقلانية من أجل استبدال التقويم الميلادي. تكونت أيام التقويم الجمهوري الفرنسي من عشر ساعات في كل منها مائة دقيقة في كل منها مائة ثانية، مما يعتبر انحرافاً عن نظام العد الاثني عشري المستخدم في العديد من الثقافات الأخرى. تم إلغاء النظام لاحقا في سنة 1806.[7]
تاريخ آلات قياس الوقت
مزولة أفقية في تاغانروغ. ساعة رملية
تم اختراع عدد كبير من أجهزة القياس بهدف قياس الوقت. يُطلق على دراسة هذه الأجهزة اسم علم البنكامات.[8]
يعود جهاز مصري إلى حوالي 1500 ق.م –شبيه بالمسطرة حرف تي- والذي كان يقيس مرور الوقت باستخدام الظل الساقط من العمود الموجود على مسطرة غير خطية. كان حرف تي يوضع شرقا في الصباح، وعند الظهر يُقلب الجهاز ليتمكن من إسقاط ظله في اتجاه المساء.[9]
تستخدم المزولة قياسا يلقي بظله على عدد من العلامات التي تمثل الساعة. يحدد مكان سقوط الظل الساعة في المنطقة الزمنية. تعود فكرة تقسيم اليوم إلى أجزاء أصغر إلى المصريين بسبب اختراعهم المزولة والتي كانت تعمل على نظام اثني عشري. ترجع أهمية الرقم اثني عشر إلى عدد الدورات القمرية في السنة وعدد النجوم المستخدمة لحساب مرور الوقت ليلا.[10]
كانت أكثر أجهزة العالم القديم دقة في قياس الوقت هي الساعة المائية والتي وُجدت واحدة منها في مقبرة الفرعون المصري أمنحتب الأول. كانت الساعة المائية تُستخدم في قياس الساعات حتى في الليل ولكنها كانت تتطلب ضبطا يدويا لاستكمال تدفق الماء. حافظ اليونانيون القدماء وشعوب كلدو (جنوب بلاد ما بين النهرين) على قيسهم للوقت كجزء أساسي في ملاحظاتهم الفلكية. قدم المخترعون والمهندسون العرب تحسينات على استخدام الساعات المائية حتى العصور الوسطى. في القرن الحادي عشر، اخترع المخترعون والمهندسون الصينيون أول ساعة ميكانيكة مبنية على آلية ميزان الساعة.
تستخدم الساعة الرملية سريان الرمل لقياس مرور الوقت. استُخدمت هذه الساعات في الملاحة. استخدم فرناندو ماجلان 18 ساعة رملية على كل سفينة عند إبحاره حول الكرة الأرضية في 1522.
كانت أعواد البخور والشمع تُستخدم لقياس الوقت في المعابد والكنائس حول العالم. كانت ساعات الماء ولاحقا الساعات الميكانيكية تُستخدم لتحديد أحداث الكنائس والأديرة في العصور الوسطى.[11] بنى ريتشارد من والينجفورد (1292-1336) ساعة ميكانيكة شهيرة كآلة فلكية في حوالي 1330.
قدم غاليليو غاليلي إسهامات ضخمة في قياس الزمن بدقة، وخاصة كريستيان هوغنس مع اختراع الساعات القائمة على البندول مع اختراع جوست بورغي لعقرب الدقائق.[12]
تأتي الكلمة الإنجليزية clock والتي تعني الساعة من الكلمة الهولندية الوسطى klocke والتي تأتي بدورها من الكلمة اللاتينية الوسطى clocca والتي أتت في آخر الأمر من اللغة الكلتية والتي تشبه الكلمات الفرنسية واللاتينية والألمانية والتي تعني الجرس. تحدد مرور الساعات في البحر بواسطة الأجراس والتي كانت تدلل على الوقت (انظر جرس سفينة). تحددت الساعات في الكنائس عن طريق الأجراس مثل البحر.
تمتد الساعات من ساعات اليد إلى الأنواع الأخرى الأكثر غرابة من الساعات. تعمل الساعات على العديد من الوسائل بما في ذلك الجاذبية والنوابض والعديد من صور القوى الكهربية، كما يضبطها العديد من الوسائل الأخرى مثل الرقاص أو البندول.[13][14]
ظهرت المنبهات لأول مرة في اليونان القديمة حوالي سنة 250 ق.م في ساعة مائية تطلق صافرة. عدل كل من ليفي هتشنز وسيث توماس لاحقا على هذه الفكرة.
الكرونومتر هو أداة محمولة لتتبع الوقت والذي لا بد أن يصل إلى بعض أسس الدقة. في البداية، استُخدم المصطلح للإشارة إلى الكرونومتر البحري وهو أداة زمنية تستخدم لتحديد الطول الجغرافي باستخدام طرق الملاحة الفلكية، والتي كان جون هاريسون أول من حقق الدقة من خلالها. حديثا، تم تطبيق المصطلح أيضا على الكرونومتر الخاص بالزمن، وهي ساعة تصل إلى بعض أسس الدقة التي تضعها الشركة السويسرية COSC.
أكثر الآلات الزمنية دقة في تتبع الوقت هي الساعة الذرية،[15] والتي تبلغ دقتها ثانية كل عدة ملايين من السنين، وتستخدم في ضبط الساعات والآلات الزمنية الأخرى.
تستخدم الساعات الذرية الانتقالات الإلكترونية في بعض الذرات لقياس الثانية. أحد أكثر الذرات المستخدمة هي ذرة عنصر السيزيوم،[16] حيث تفحص معظم الساعات الذرية الحديثة السيزيوم بموجات الراديو لتحدد تردد اهتزازات هذه الإلكترونات. منذ 1967، حددت المنظمة الدولية للقياسات وحدة الزمن (الثانية) بناء على خواص ذرات السيزيوم. يعرف نظام الوحدات الدولي الثانية بأنها 9,192,631,770 دورة للإشعاع المقابل للانتقال بين مستويي طاقة للإلكترون من الحالة الأرضية لذرة السيزيوم.
اليوم يمكن استخدام نظام التموضع العالمي بالتنسيق مع بروتوكول وقت الشبكة لتوقيت وتزامن أنظمة قياس الوقت حول العالم.
في الكتابات الفلسفية من العصور الوسطى، كانت الذرة هي وحدة قياس الزمن حيث كان يُشار إليها بأنها أصغر وحدة ممكنة من الزمن. أول ذكر للكلمة في الإنجليزية في كتابات بيرثفيرث (كتاب علمي) في حوالي 1010-1012 حيث عرفها بأنها 1/564 من فترة الزخم (دقيقة ونصف) وبالتالي يساوي 15/94 من الثانية.[17]
منذ مايو 2010، أصبحت أصغر وحدات تقسيم الزمن هو الأس 12 للأتوثانية (1.2 × 10−17 ثانية) وهي حوالي 3.7 × 1026 من زمن بلانك.[18]
وحدات الزمن
الثانية هي الوحدة الأساسية لنظام الوحدات الدولي. الدقيقة هي 60 ثانية، والساعة تبلغ 60 دقيقة. يبلغ اليوم 24 ساعة أو 86,400 ثانية.
الدين
الزمن الخطي والزمن الدوري
كان للعديد من الحضارات القديمة مفهوم عجلة الزمن مثل الإنكا والمايا والهوبي والقبائل الأخرى في أمريكا الوسطى، بالإضافة إلى البابليين واليونانيين القدماء والهندوسيين والبوذيين والجاينيين وغيرهم، حيث اعتبروا الزمن على أنه تعاقب دوري ومتجانس ويتكون من أعمار متكررة تحدث لكل كائن حي في الكون ما بين مولده ووفاته.[19]
بشكل عام، يعتبر التراث الإسلامي والتراث اليهودي المسيحي أن الزمن يسير بصورة خطية واتجاه نسبي، حيث بدأ بفعل الخلق بواسطة الله. يرى التراث المسيحي التقليدي أن الزمن ينتهي (لاهوتيا) مع الإسخاتولوجيا المسيحية ونهاية النظام الحالي للأشياء أو ما يُعرف باسم «نهاية الزمان». في العهد القديم كتاب سفر الجامعة والمنسوب تقليديا إلى سليمان (970-928 ق.م)، اعتُبر الزمن (أو الكلمة العبرية זמן)وسيلة لإنفاذ أحداث القدر.[20]
الزمن في الميثولوجيا اليونانية
تفرق اللغة اليونانية بين مبدأين منفصلين: خرونوس وكايروس. يشير الأول إلى الزمن العددي أو التقويمي، بينما يشير الأخير (حرفيا اللحظة الحالية) إلى الزمن الإلهي أو الميتافيزيقي. في اللاهوت، كايروس قابل للتعداد على عكس خرونوس.
في الميثولوجيا اليونانية، كرونوس (باليونانية القديمة: Χρόνος) هو تشخيص الزمن. اسمه في اليونانية يعني «الزمن». عادة ما كان يتم تشخيص الزمن على أنه رجل عجوز حكيم له لحية طويلة رمادية.
الزمن في القبالة
طبقا للقبالة اليهودية، فالزمن مفارقة[21] ووهم،[22] فكل من المستقبل والماضي هي أحداث حاضرة مجمعة.
الفلسفة
"الزمن ليس مفهوما تجريبيا، فلا يمكننا تصور التواجد أو التتابع إن لم يوجد مفهوم الزمن كبديهة أساسية. بدون هذا الافتراض المسبق لن يكون بإمكاننا التمثيل لأنفسنا أن هناك أشياء تتواجد معا وفي نفس الوقت، أو في أوقات مختلفة، بعبارة أخرى متعاصرة أم متتالية".
“
”
إيمانويل كانت، نقد العقل المحض.
ينقسم الفلاسفة إلى رأيين متضادين بخصوص الزمن. أحد الرأيين هو جزء من التركيب الأساسي للفضاء الكوني أو بُعد مستقل عن الأحداث والذي تحدث فيه الأحداث متتالية. كان إسحق نيوتن أحد مناصري هذا الرأي الواقعي، ومن هنا أصبح يُشار إلي ذلك الرأي باسم الزمن النيوتوني.[23][24] الرأي المقابل هو أن الزمن لا يشير إلى أي نوع من «الاحتواء» والذي «تتحرك» الأشياء والأحداث خلاله، ولكنه جزء من بناء عقلي أساسي (مع المكان والعدد) والذي تحدث فيه أفعال وأحداث البشر. يرى هذا الرأي الثاني (مثل غوتفريد لايبنتس وإيمانويل كانت[25]) أن الزمن ليس بحدث أو شيء، وبالتالي فهو غير قابل للقياس في حد ذاته كما لا يمكن السفر عبره.[26]
علاوة على ذلك، ربما يكون هناك مكون ذاتي للزمن ولكن سواء لا تزال إمكانية الإحساس بالزمن كشعور أو كتقييم مسألة تخضع للكثير من الجدل.
تصف نصوص فيدا (أقدم النصوص التي تتحدث عن الفلسفة الهندية والفلسفة الهندوسية والتي ترجع إلى الألفية الثانية قبل الميلاد[27]) علم الفلك الهندي القديم، وفيها يمر الكون بسلسلة متكررة من الخلق والتدمير والبعث حيث تستغرق كل دورة 4,320 مليون سنة. كتب الفلاسفة اليونانيون القدماء (مثل بارمينيدس وهرقليطس) مقالات عن طبيعة الزمن. عرّف أفلاطون (في طيماوس) الزمن بأنه فترة حركة الأجسام السماوية. عرّف أرسطو (في الكتاب الرابع من السماع الطبيعي) الزمن بأنه عدد من الحركات بالنسبة إلى ما قبل وما بعد.
في الكتاب الحادي عشر من اعترافات القديس أوغسطين، يتأمل أوغسطين في طبيعة الزمن متسائلا: «إذا ما هو الزمن؟ إن لم يسألني أحد، فانا أعرف أنني أتمنى أن أفسر ذلك في حال سألني أحدهم» يشرع أوغسطين بعد ذلك في تعريف الزمن بما لا يعتبر منه بدلا من ما يعتبر منه، وهو أسلوب مشابه للأسلوب الذي اتبعه في التعريفات السالبة.[28] إلا أن القديس أوغسطين انتهى بأن أطلق على الزمن بأنه «تمدد» للعقل والذي من خلاله نستوعب الماضي في ذاكرتنا، والحاضر في انتباهنا، والمستقبل في توقعنا، كل ذلك في نفس الوقت.
تتشارك الأديان الإبراهيمية في هذا المعتقد حيث تعتقد جميعها أن الزمن الكوني بدأ مع الخلق.[بحاجة لتوضيح]
آمن إسحق نيوتن بالمكان المطلق والزمان المطلق، بينما آمن لايبنتس بأن الزمان والمكان نسبيين. برزت الاختلافات بين تفسيرات نيوتن ولايبتس في مراسلات لايبتس كلارك الشهيرة.[29]
وصف إيمانويل كانت –في نقد العقل المحض- الزمن بأنه فكرة بديهية تسمح لنا (مع الفكرة البديهية الأخرى: المكان) باستيعاب الأدلة التجريبية. يعتقد كانت أنه لا المكان ولا الزمان يمكن تصوره كحركة جوهرية، ولكن كلا منهما إطار عقلي نظامي والذي ينشئ أي تجربة عقلية أو ملاحظة تجريبية. رأى كانت الزمن كجزء أساسي من الإطار العقلي للبنية المجردة –مع المكان والعدد- والذي نستخدمه في تسلسل الأحداث، وجعلها كمّية خلال مدتها، ومقارنة حركة الأشياء
أخيرا هذه زبدة البحوث العلمية حول هذا الموضوع نضعها للقاريء والباحث لكي يكون أطلاع واسع على العلوم العصرية والتقنيات الحديثة .





